QL-P12

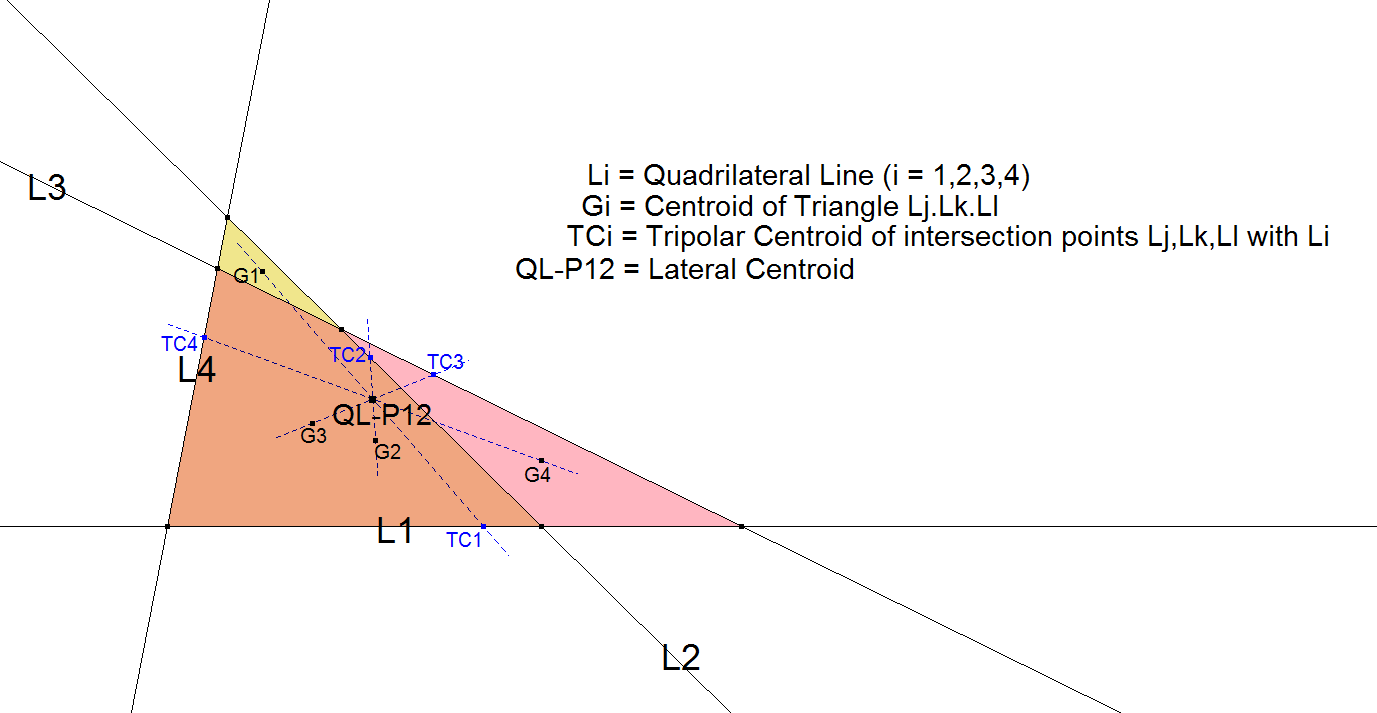
QL-P12: QL-Centroid or Lateral Centroid

QL-P12 is the Centroid of the six intersection points of the 4 defining QL-Lines as mentioned by J.W. Clawson. See Ref-31, page 41.

It is called the Lateral Centroid because it is constructed in the Quadrilateral environment.

It can be constructed as the midpoint of any set of two triangles formed from the six intersection points.

Just like in the QA-environment, the Centroid in the QL-environment is the Midpoint of 1^st and 2^nd Quasi Centroids.

Other ways of construction:

QL-P12 is the Tripolar Centroid ^*) of the QA-Centroids in the 3 QL-Quadrigons.
Let Gi be the Centroid of component triangle Lj.Lk.Ll and let Gjkl be the Centroid of Centroids Triangle Gj.Gk.Gl , where (i,j,k,l) ∈ (1,2,3,4). Lines Gi.Gjkl concur in QL-P12.
Let Gi be the Triangle Centroid (X2) of Triangle Lj.Lk.Ll. Let TCi be the Tripolar Centroid *) of the 3 intersection points of Lj, Lk, Ll with Li. Now all lines Gi.TCi (i=1,2,3,4) concur in QL-P12.
QL-P12 is the homothetic Center of the Reference Quadrilateral L1.L2.L3.L4 and the homothetic Quadrilateral formed by the lines parallel to the lines L1, L2, L3, L4 through the Centroids of the corresponding component triangles.
QL-P12 is the Quadrangle Centroid (QA-P1) of the Centroid Quadrangle of the Reference Quadrilateral (note Seiichi Kirikami).
QL-P12 is also mentioned by J.W. Clawson (see Ref-31) as the Centroid of the Triangle formed by the 3 QL-points QL-P2, QL-P4 and QL-P5.

*) The Tripolar Centroid is the Centroid of a “flat” triangle formed by 3 collinear points.

Construction-method: Suppose P, Q, R are collinear points not on the line at infinity. Let M = Midpoint(Q, R).

The segment PM has two trisectors. The trisector closer to M is the Tripolar Centroid.

Coordinates:

1st CT-coordinate:

(m - n) (l (l + m + n) - 3 (l m + l n - m n)) (note that this formula is independent of a,b,c)

1st DT-coordinate:

(m²-n²) (m² (l²-n²) + n² (l²-m²))

Properties:

– QL-P2.QL-P6 ( 2 : 1)

– QL-P5.QL-P7 = QL-L1

– QL-P8. QL-P14 = QL-L8 ( 3 : 1)

– QA-P10. QG-P4 ( 1 : 1 => QL-P12 = Midpoint QA-P10 and QG-P4)

– QA-P26. QG-P8 (-1 : 3)

QL-P12 is the Midpoint of QL-P14 (1^st QL-Quasi Centroid) and QL-P15 (2^nd QL-Quasi Centroid).
QL-P12 is the Midpoint of QL-P8 and QL-P18.
The distance ratios between points QL-P20, QL-P22, QL-P12, QL-P5 are 3 : 1 : 2.
d(QL-P6 , QL-P12) = d(QL-P2 , QL-P12) / 2. (d = distance)
d(QL-P5 , QL-P12) = d(QL-P2 , QL-P3) / 3.
QL-P12 is the point where the sum of the squares of the distances to the 6 intersection points of the Reference Quadrilateral is minimal.
QA-P26 is the Centroid of the Triangle formed by the 3 QL-versions of QL-P12 (note Eckart Schmidt).
QL-P12 is the Centroid of the 3 Triangles being the 3 QL-versions of QL-P8, QG-P4, QA-P10 (all Centroid related points).
QL-P12 is the Centroid of the Triangle formed by the 3 QL-points QL-P2, QL-P4, QL-P5 (J.W. Clawson, see Ref-31).
QL-P12 is the Centroid of QL-Tr2.
QL-P12 lies on the Polar (see Ref-13, Polar) of QL-P18 wrt QL-Co1 and vice versa.
QL-P12 lies on the Polar (see Ref-13, Polar) of QL-P13 wrt QL-Co2 and vice versa.
Let X2i (i=1,2,3,4) be the circumcenters of the triangles (Lj,Lk,Ll), where j,k,l=different numbers from (1,2,3,4) unequal i. Let L2i be the lines through X2i parallel to Li. QL-P12 is the Homothetic Center of the Reference Quadrilateral and (L21,L22, L23, L24). This construction is similar to the construction of QL-P20 and QL-P22.

MATHEMATICS