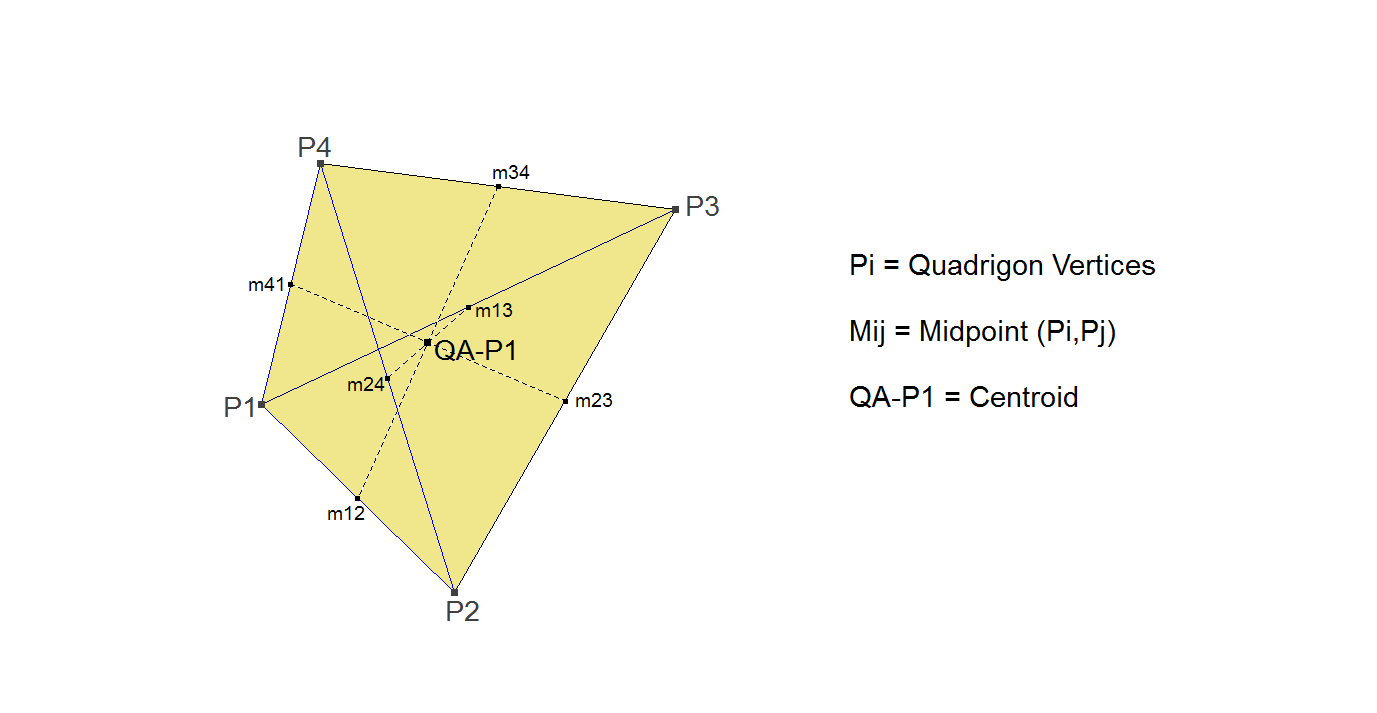
QA-P1: QA-Centroid or Quadrangle Centroid
The Centroid of a Quadrangle is actually the center of gravity of a Quadrangle, replacing the points by equal masses.
The usual way to construct it is by connecting midpoints of opposite sides of a chosen component Quadrigon. The two connecting lines as well as the line connecting the midpoints of the diagonals meet at the Centroid.
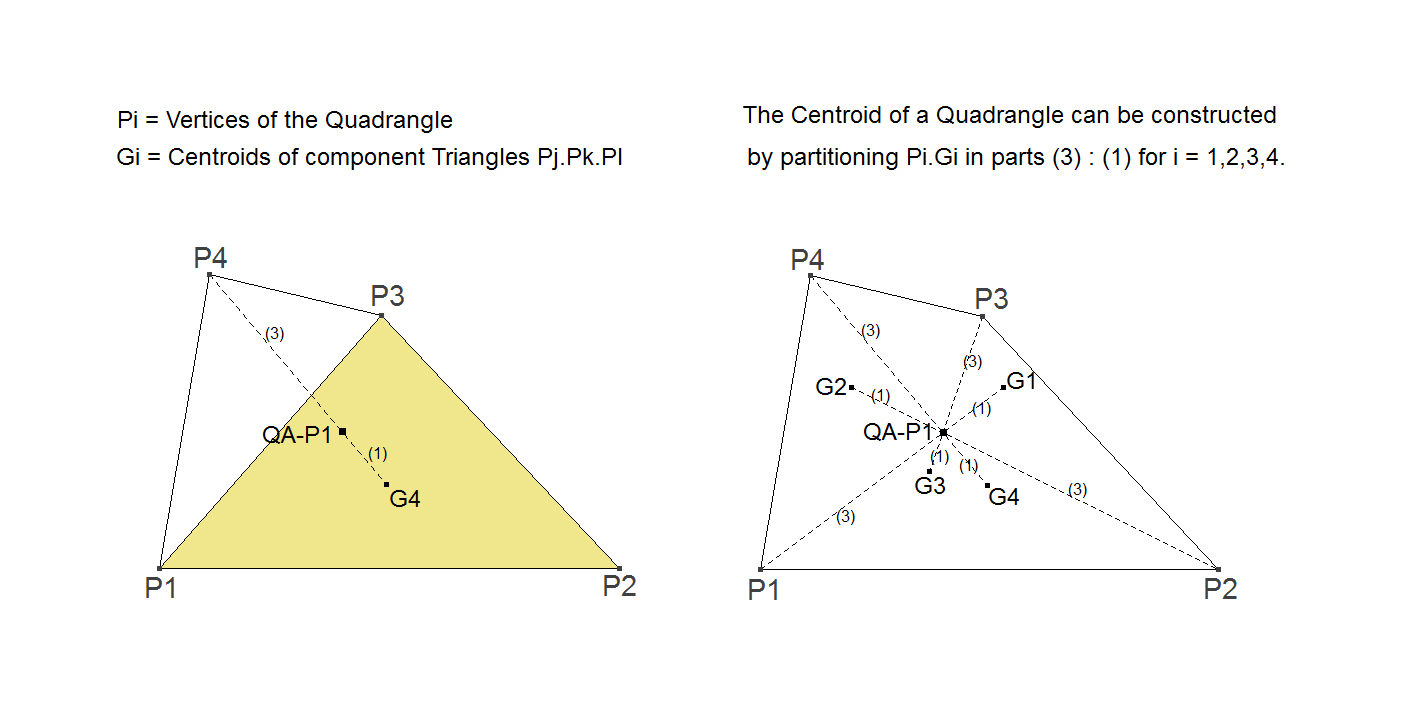
However there is also another way to construct the Quadrangle Centroid using component triangles. This way of construction makes it clear that it really is a Quadrangle Center because it can be constructed in the same way for all component triangles of the Quadrangle. This picture shows that the Centroid can be constructed by partitioning Gi.Pi in parts 3 : 1.
1st CT-Coordinate
2 p + q + r
1st DT-Coordinate
p2 (-p2 + q2 + r2)
Properties
- QA-P1 lies on these QA-lines:
- QA-P1 lies on these QG-lines:
- QA-P1 = Center of the Nine-point Conic QA-Co1.
- QA-P1 = QA-P10-Ceva conjugate of QA-P16 wrt the QA-Diagonal Triangle.
- QA-P1 = the Involutary Conjugate (see QA-Tf2) of QA-P20.
- QA-P1 = Homothetic Center of the 1st Nine-point Quadrangle and the 1st Midray Quadrangle.
- QA-P1 = the point of tangency of the two congruent tangent circumcircles of the triangles defined by the 3 QA-versions of QG-P7 (1st Quasi Nine-point Center) and the 3 QA-versions of QG-P9 (2nd Quasi Circumcenter).
- QA-P1 = QA-Centroid (QA-P1) of the quadrangle formed by the vertices of the Diagonal Triangle and QA-P5.
- QA-P1 = Gergonne-Steiner (QA-P3) point of the quadrangle formed by the vertices of the Diagonal Triangle and QA-P3.
- QA-P1 is the Euler-Poncelet Point (QA-P2) of the Nine-point Center Quadrangle (Eckart Schmidt, August 24, 2012).
- The 3 QL-versions of QA-P1 lie on the Newton Line QL-L1.
- QA-P1 lies on the Circle defined by the 3 QA-versions of QG-P9 (note Eckart Schmidt).
- QA-P1 lies on the Conic QA-Co5.
- QA-P1 lies on the Conic through P1, P2, P3, P4 and QA-P16.
- QA-P1 lies on the Cubics QA-Cu2, QA-Cu3, QA-Cu5, QA-Cu6.
- QA-P1 has the property of Least Squares Distance (LSD) from P1, P2, P3 and P4. And it also has the property of Least Squares Distance (LSD) from Midpoints M12, M13, M14, M23, M24 and M34 (Seiichi Kirikami, April 3, 2013).
- QA-P1 is the QA-Orthopole (QA-Tf3) of QA-P3. The QA-Orthopole of QA-P1 is the Midpoint (QA-P1,QA-P23).
- The QA-Orthopole(QA-Tf3) of QL-Ci6 is a circle through QA-P1.
- QA-P1 is the Parallelologic Center of the Triple Triangles of QG-P7/QG-P9 wrt the Triple Triangles of QG-P5/QG-P10/QL-P2 Triple Triangle (see QA-Tr-1).
- QA-P1 is the Orthology Center of the Triple Triangles of QG-P2/QG-P12/QL-P5/QL-P7/QL-P12/QL-P20/QL-P22/QL-P23 wrt the Triple triangles of QG-P5/QG-P10/QL-P2. See QA-Tr-1.
- QA-P1 is the Perspector of the mutual Triple Triangles (see QA-Tr-1) of QG-P2, QG-P12, QL-P5, QL-P7, QL-P12, QL-P20, QL-P22, QL-P23.
- QA-P1 is the Perspector of the mutual Triple Triangles (see QA-Tr-1) of QG-P1, QG-P4, QG-P8, QG-P15.
- QA-P1 is the Perspector of the QG-P5 Triple Triangle and the QG-P10 Triple Triangle (see QA-Tr-1).
- QA-P1 is the Perspector of the QG-P7 Triple Triangle and the QG-P9 Triple Triangle (see QA-Tr-1).
Estimated human page views: 1762
