nP-n-Tf2 nP-Linear Pole
nP-n-Tf1 is the generalization of the trilinear pole (also called tripole) in a triangle.
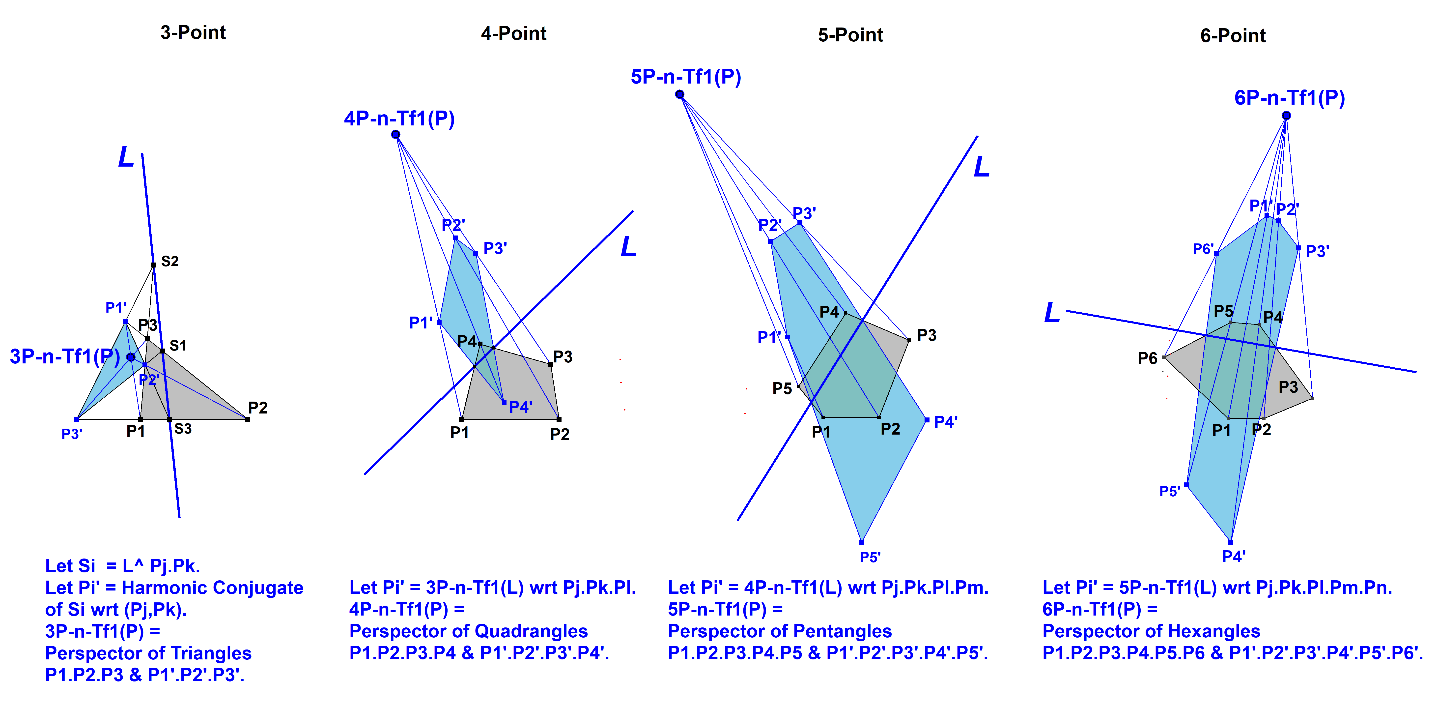
nP-n-Tf1 transforms a random line L into an “nP-Linear Pole”, which is a point in an n-Point.
In a 3-Point it is the well-known Trilinear Pole in the Triangle, also called Tripole. See Ref-13.
In a 4-Point it is the OA-Trilinear Pole (QA-Tf7) in the Quadrilateral which was found by Tran Quang Hung. See [34], QFG#2084. It is derived from the Tripole.
The method for constructing the nP-Linear Pole in an n-Point for n>4 is done in a recursive way by using the same “upgrading-method” as used for deriving the n=4 case. See figure below.
Correspondence with ETC/EQF
Properties
- nP-n-Tf1 is the dual of nL-n-Tf5, because when the notions of “Points” and “Lines” are interchanged in the description of the construction and “the intersection of two lines” and “the connection of two points” are interchanged, then the other transformation pops up, which makes them duals.
Estimated human page views: 138
