nP-n-P4 nP-MVP-Nine-point Center
nP-n-P4 is the nL-Mean Vector Point of X(4), the Triangle Nine-point Center.
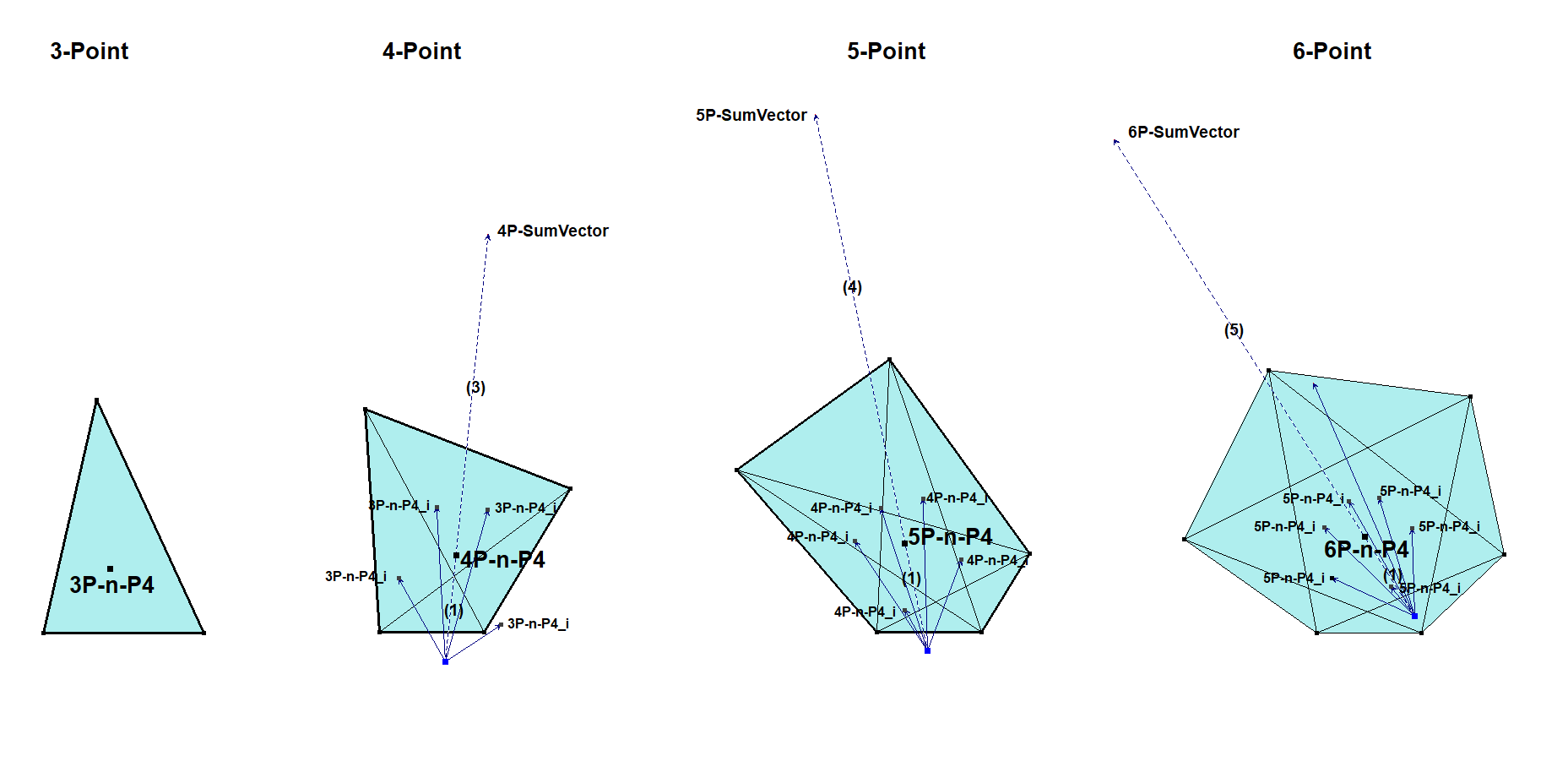
In this method central points from ETC are successively constructed in higher level n-Point figures starting with n=3, then n=4 using the results of n=3, then n=5 using the results of n=4, etc.
See nP-n-Luc1 for a detailed description.
Correspondence with ETC/EQF
In a 3-Point:
- 3P-n-P1 = 3P-MVP Centroid = X(2)
- 3P-n-P2 = 3P-MVP Circumcenter = X(3)
- 3P-n-P3 = 3P-MVP Orthocenter = X(4)
- 3P-n-P4 = 3P-MVP Nine-point center = X(5)
In a 4-Point we find:
- 4P-n-P1 = 4P-MVP Centroid = QA-P1 (QA-Centroid)
- 4P-n-P2 = 4P-MVP Circumcenter = QA-P32 (Centroid Circumcenter Quadrangle)
- 4P-n-P3 = 4P-MVP Orthocenter = QA-P33 (Centroid Orthocenter Quadrangle)
- 4P-n-P4 = 4P-MVP Nine-point center = Midpoint (QA-P32,QA-P33)
Properties
- nP-n-P1, nP-n-P2, nP-n-P3 and nP-n-P4 are collinear on nP-n-L1. Their mutual distance ratios correspond with the mutual distance ratios from triangle centers X(2), X(3), X(4) and X(5).
Estimated human page views: 318
