nP-n-L1: nL-MVP Eulerline
The nL-MVP Eulerline is the line connecting collinear points nP-n-P1, nP-n-P2, nP-n-P3, nP-n-P4, being the MVP-Centroid, Circumcenter, Orthocenter and Nine-point Center in an n-Point.
For an explanation of MVP-points see nP-n-Luc1.
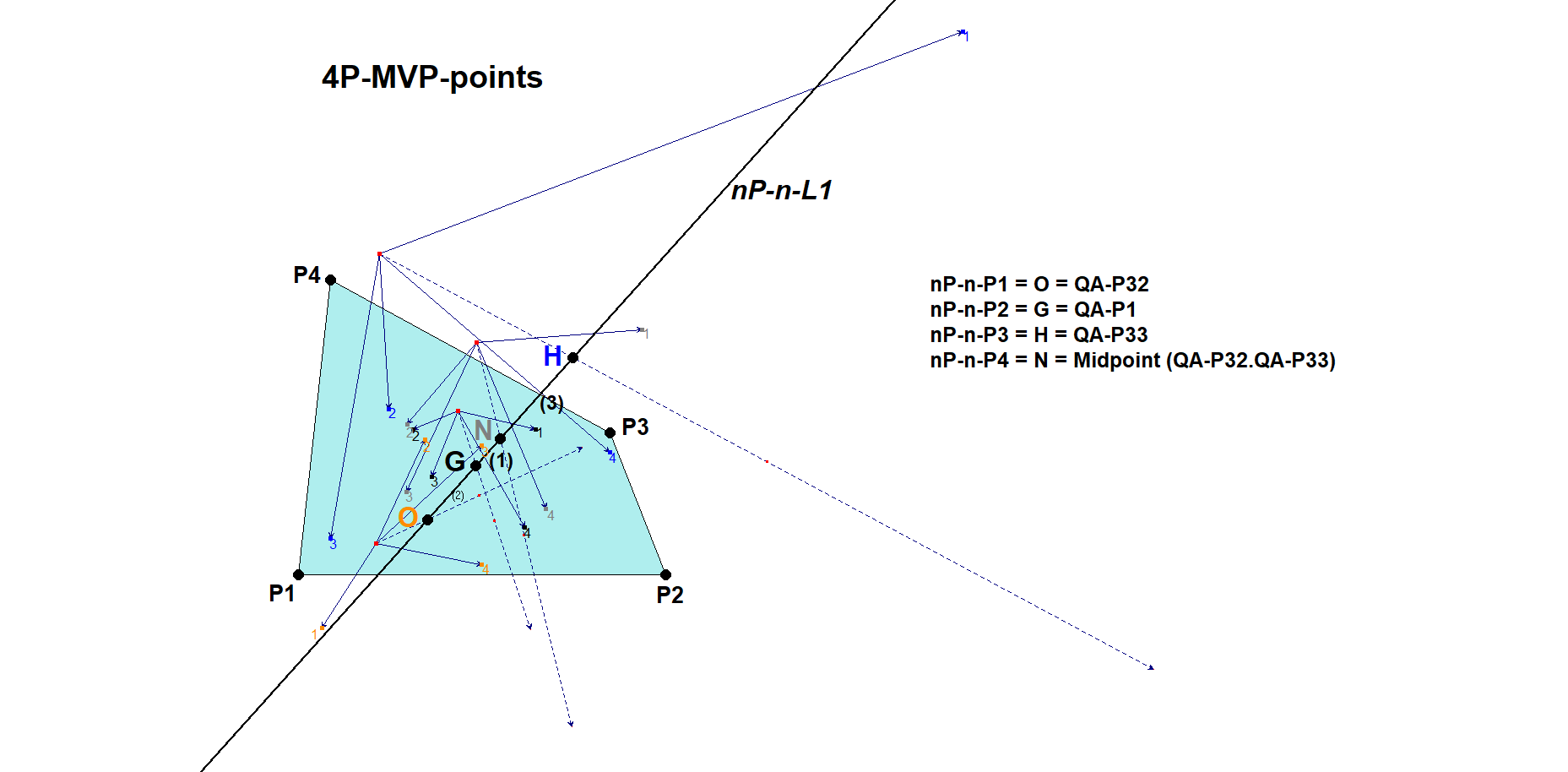
Next figure gives an example of nP-n-L1 in a 4-Point.
Correspondence with ETC/EQF
When n=3, then nP-n-L1 = Triangle Eulerline X(3).X(4), with
- 3P-n-P1 = 3P-MVP Centroid = X(2)
- 3P-n-P2 = 3P-MVP Circumcenter = X(3)
- 3P-n-P3 = 3P-MVP Orthocenter = X(4)
- 3P-n-P4 = 3P-MVP Nine-point center = X(5)
When n=4, then nP-n-L1 = Quadrilateral Eulerline QA-P1.QA-P32.QA-P33, with
- 4P-n-P1 = 4P-MVP Centroid = QA-P1 (QA-Centroid)
- 4P-n-P2 = 4P-MVP Circumcenter = QA-P32 (Centroid Circumcenter Quadrangle)
- 4P-n-P3 = 4P-MVP Orthocenter = QA-P33 (Centroid Orthocenter Quadrangle)
- 4P-n-P4 = 4P-MVP Nine-point center = Midpoint (QA-P32,QA-P33)
Properties
Estimated human page views: 325
