9P-s-Cu1 9P-Cubic
A cubic in general is defined by 9 random points.
A cubic with 7 random points and the 2 imaginary circular points at infinity is called a circular cubic and can be found at 7P-s-Cu1.
Construction
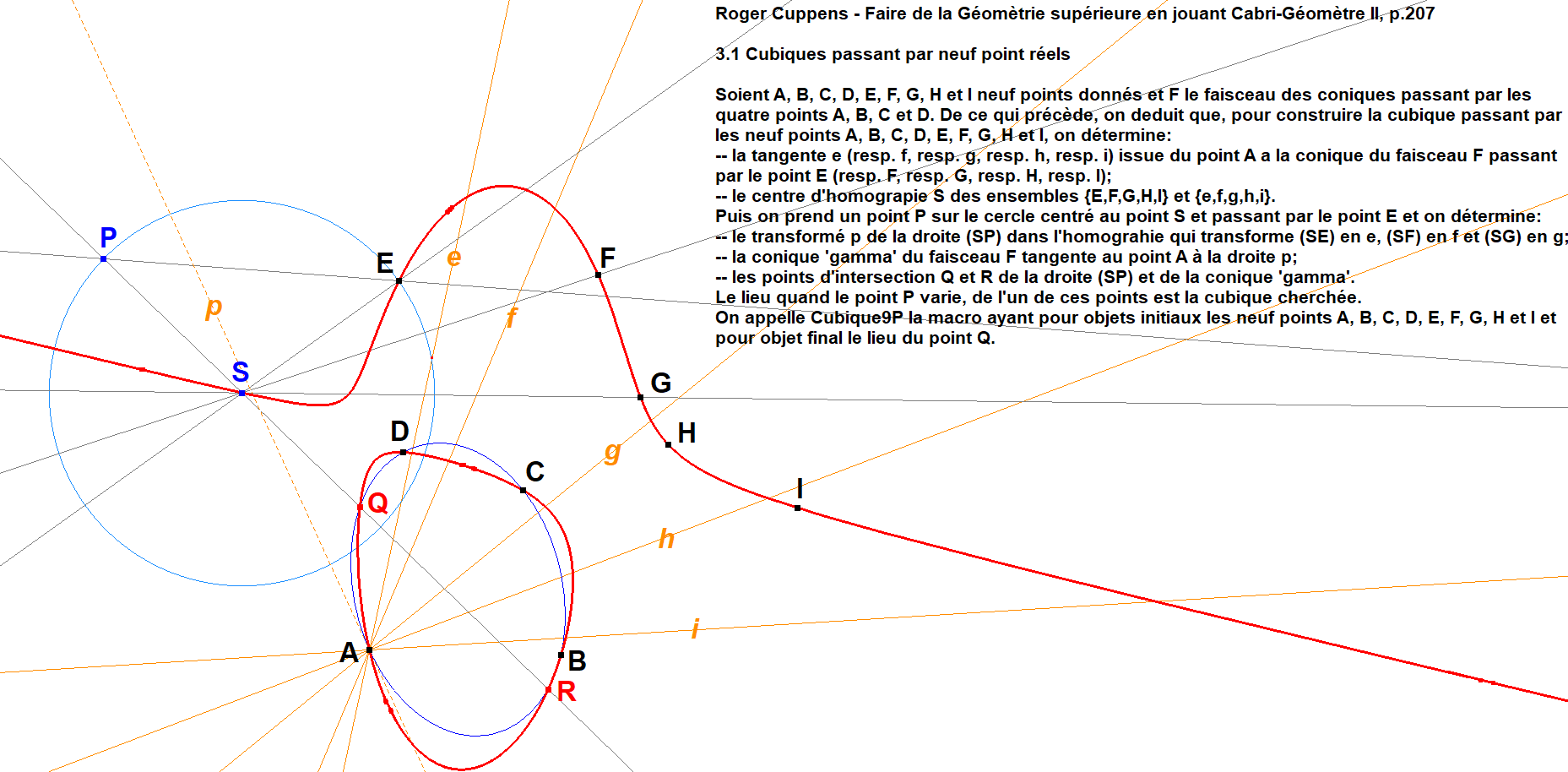
See picture and [63], page 207.
See also remarks at 7P-s-Cu1.
Properties
- A regular cubic is determined by 9 points. Through 8 random points infinitely many cubics can be drawn. However according to the Cayley-Bacharach theorem they will all pass through a common point, named the Cayley-Bacharach point (8P-s-P1). Therefore by varying one defining point P9 on the cubic many new cubics will occur with one common point 8P-s-P1 (apart from the other 8 defining points). And therefore each point on a cubic has a corresponding Cayley-Bacharach point. See also 7P-s-Tf1.
- When the cubic is circular (see 7P-s-Cu1) then there is the corresponding Cayley-Bacharach point 6P-s-P2. See also 5P-s-Tf1.
Estimated human page views: 200
