6P-s-P1 6P-Schmidt Point
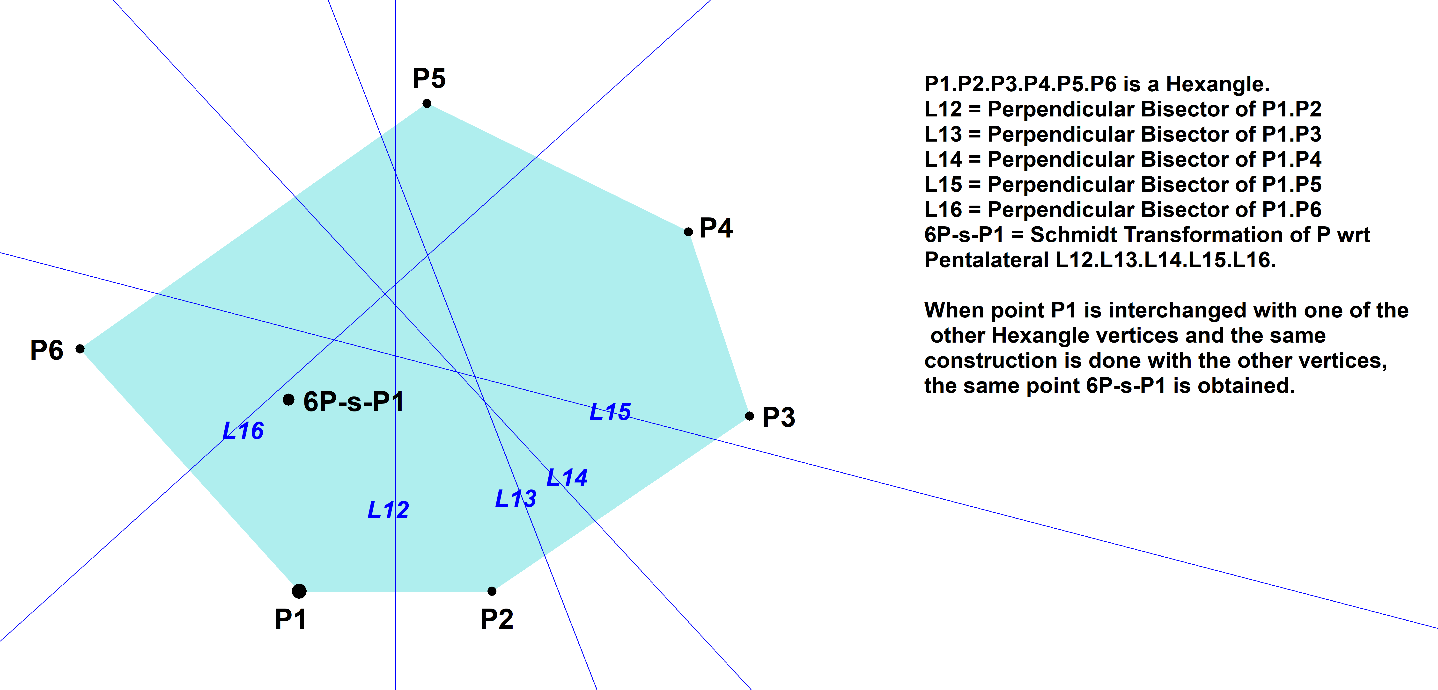
Consider a 6-Point (Hexangle) with vertices Pi (i=1,2,3,4,5,6).
Choose one of its vertices Pi.
Construct the perpendicular bisectors Lij of (Pi,Pj), where j unequal i.
In this way Pi defines a 5-Line (Pentalateral) formed by these perpendicular bisectors.
It appears that the 5L-Schmidt Transformation (5L-s-Tf1) wrt this 5-Line of Pi is independent of the chosen Pi. This fixed point is 6P-s-P1.
This point was found by Eckart Schmidt. See [34], QFG #3551.
Properties
- 6P-s-P1 is the center of the 6P-CSC Circle (6P-s-Ci1).
Estimated human page views: 274
