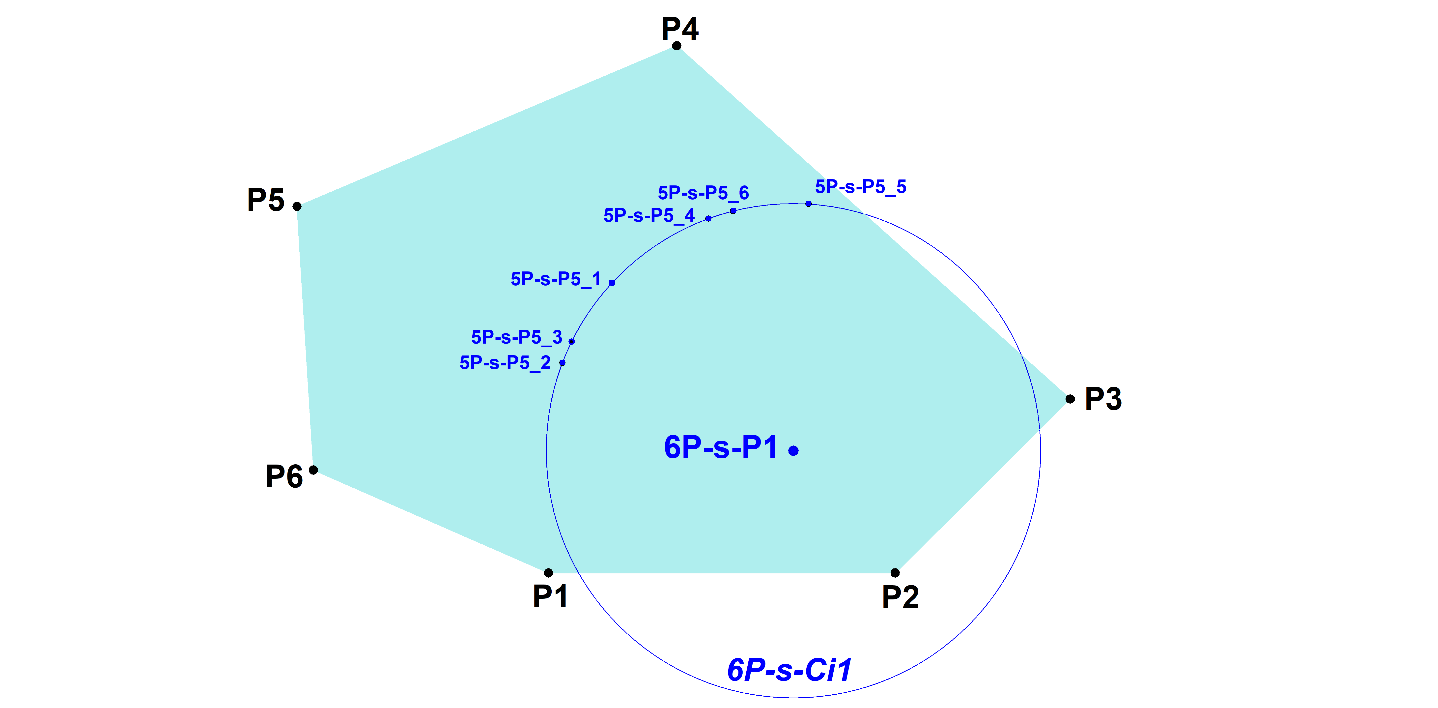
6P-s-Ci1 6P-CSC Circle
A 6-Point has 6 Component 5-Points.
The 6 versions of 5P-s-P5 (5P-Schmidt Point) lie on a circle in a 6-Point being 6P-s-Ci1.
This circle is mentioned by Eckart Schmidt and called the CSC-circle because it came up in a problem where it had the function of the Clawson-Schmidt Conjugate (CSC). See [34], QFG-messages #3575, #3579, #3586-3588, #3618.
Properties
- The center of the circle is 6P-s-P1 (6P-Schmidt Point).
- In a 7-Point the 7 versions of 6P-s-Ci1 have one common point, which is 7P-s-P1 (7P-Schmidt Point).
- All points in the plane mapped by 6P-s-Tf1 lie on 6P-s-Ci1. Exceptions are the 6P-vertices and points lying on lines Pi.Pj, their images are indetermined. See [66], QPG-message #653, #654 and #657.
- When we consider a circular cubic Cux = 7P-s-Cu1(P1,P2,P3,P4,P5,P6,Px), where Px is some point on 6P-s-Ci1, then 6P-s-Tf1(X) = 6P-s-Tf1(Px) for all points X on Cux. Hence we have a pencil of circular cubics, all passing through 6P-s-P2 and each corresponding with its own unique point on circle 6P-s-Ci1. See [66], QPG-message#653 and #657.
Estimated human page views: 217
