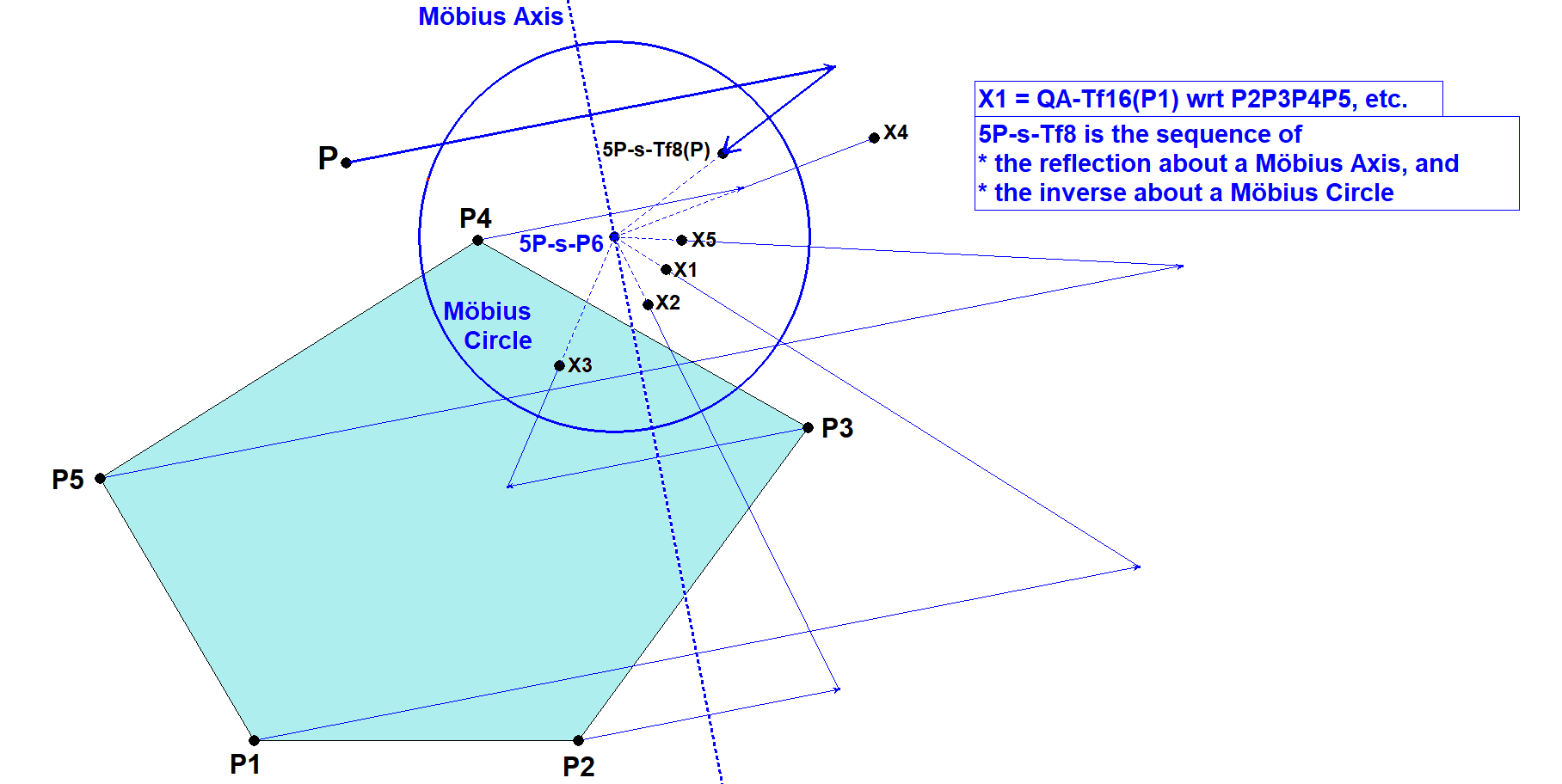
5P-s-Tf8 is a Möbius transformation, centered in 5P-s-P6, swapping P1 and X1=QA-Tf16(P1), P2 and X2=QA-Tf16(P2), P3 and X3=QA-Tf16(P3), P4 and X4=QA-Tf16(P4), P5 and X5=QA-Tf16(P5),
where QA-Tf16 is performed wrt the quadrangle of the 4 vertices unequal Pi.
That very Möbius transformation also can map other points P and is called the 5P-CSC Conjugate. It was found by Bernard Keizer and Eckart Schmidt searching for the background of 5 mysterious points, being the 5 common points of the 3 QL-versions of the cubic QA-Cu7. It turned out that for these 5 common points 5P-s-Tf8 is the Clawson-Schmidt Conjugate (CSC or QL-Tf1) of this QL. See Ref-34, QFG-messages #3266, #3270 and #3285.
where QA-Tf16 is performed wrt the quadrangle of the 4 vertices unequal Pi.
That very Möbius transformation also can map other points P and is called the 5P-CSC Conjugate. It was found by Bernard Keizer and Eckart Schmidt searching for the background of 5 mysterious points, being the 5 common points of the 3 QL-versions of the cubic QA-Cu7. It turned out that for these 5 common points 5P-s-Tf8 is the Clawson-Schmidt Conjugate (CSC or QL-Tf1) of this QL. See Ref-34, QFG-messages #3266, #3270 and #3285.
About the Möbius Transformation
A Möbius Transformation transforms generalized circles into generalized circles. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
However it preserves the angles between the intersection of circles. See Ref-35.
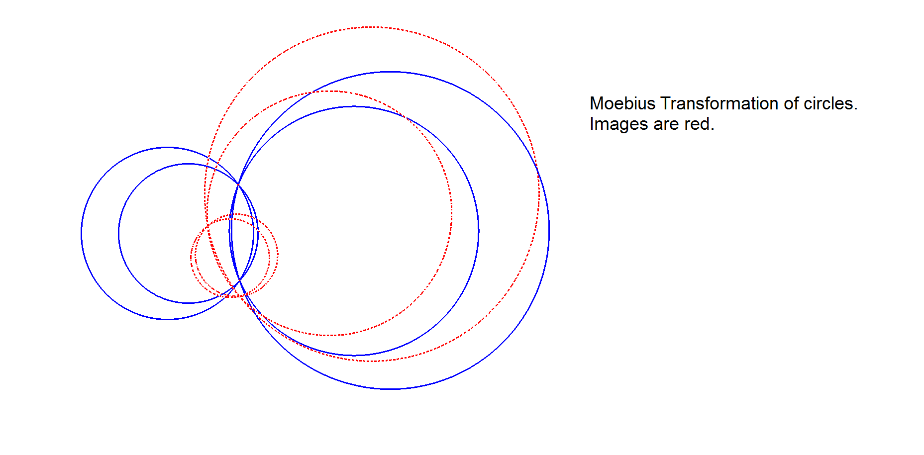
That’s what the transformation does.The transformation itself can be described as the sequence of a circle inversion and the reflection about a line through the center of this circle. The reverse order of this sequence yields the same result. See also QL-Tf1 and QA-Tf4.
Therefore, when describing a Möbius Transformation, we need to know the standard circle and its center and the line to reflect about.
Construction
We know that the pair (P1,X1) is swapped by the Möbius Transformation 5P-s-Tf8 as well as the pairs (P2,X2), (P3,X3), (P4,X4), (P5,X5). For the construction of the involved Möbius Transformation it is enough to know two swapped pairs (P1,X1), (P2,X2).
The general construction is then described in next picture.
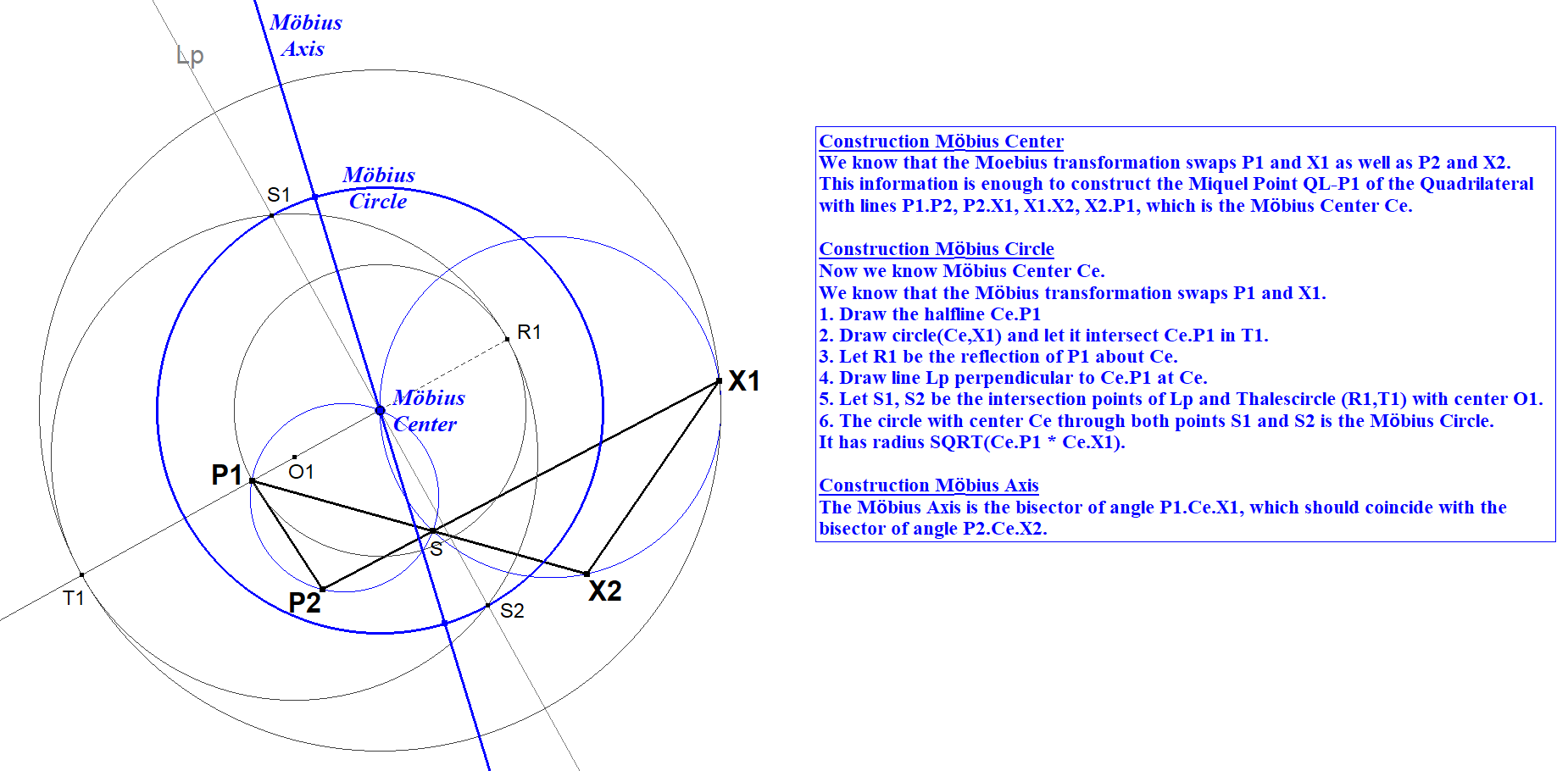
After the construction of the Möbius Center, Circle and Axis it can be checked that indeed all pairs (P1,X1), (P2,X2), (P3,X3), (P4,X4), (P5,X5) are swapped following the construction.
Properties:
• The Reference Pentangle P1P2P3P4P5 is transformed into Pentangle X1X2X3X4X5. Both Pentangles share the same 5P-s-P6. Moreover 5P-s-Tf8 wrt X1X2X3X4X5 is also a Möbius transformation, centered in 5P-s-P6, swapping Xi and Pi=QA-Tf16(Xi).
• Having X1 = QA-Tf16(P1) wrt P2P3P4P5, you have immediately X2, X3, X4 and X5 as inverses of X1 wrt the circumcircles P3P4P5, P2P4P5, P2P3P5 and P2P3P4. Conversely, the points P1 and P2 are inverse wrt the circumcircle X3X4X5 (It is a well-known and easy to prove geometrically property of the Möbius Transformation : the transformed of 2 points inverse wrt a circle are themselves inverse wrt the transformed of the circle). See Ref-34, QFG-message #3266 and Ref-66, QPG-message #626.