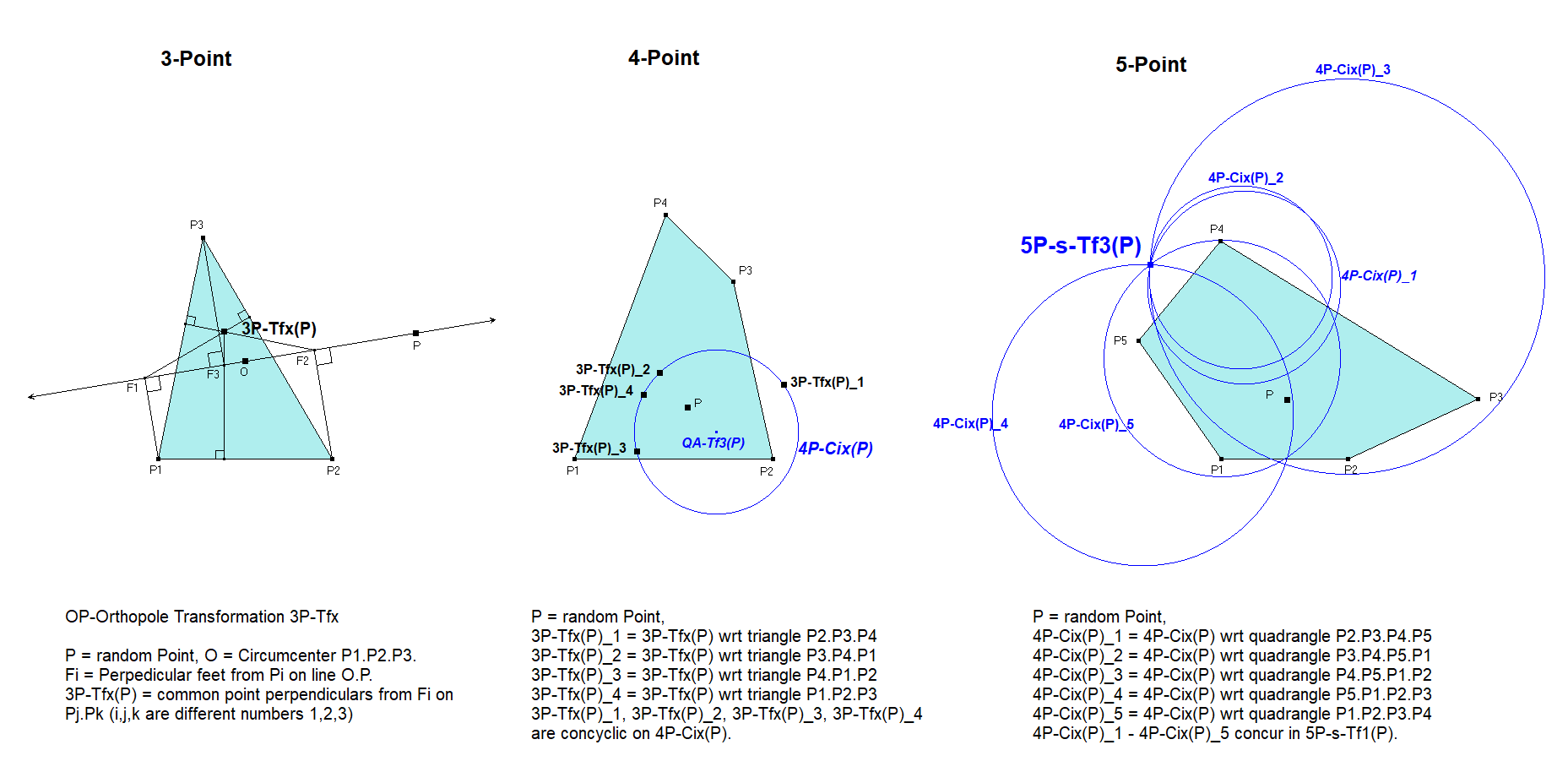
5P-s-Tf3: 5P-Orthopole
A Pentangle contains 5 Quadrangles.
Each Quadrangle contains 4 Component Triangles.
Let Oi be the Circumcenters of Component Triangles Tr_i in a Quadrangle (i=1,2,3,4).
Let P be some random point. Let Qi be the Orthopole (see Ref-13) of line P.Oi wrt Triangle Tr_i.
The 4 Orthopoles Qi of P wrt Tr_i will be concyclic on an Orthopole Circle QA-Cix (described in QA-Tf3).
Since a Pentangle contains 5 Quadrangles a random point P will generate 5 Orthopole Circles QA-Cix in a Pentangle.
These 5 Orthopole Circles QA-Cix concur in a single point which is 5P-s-Tf3(P).
This 5P-transformation was found by Telv Cohl. See Ref-33, Anopolis#1986.
As can be seen from the coordinate below 5P-s-Tf3 is a linear transformation.
1st Coordinate mapped point
Let P1,P2,P3,P4,P5, P have these barycentric coordinates:
P1=(0:1:0), P2=(0:0:1), P3=(1:0:0), P4=(p:q:r), P5=(P:Q:R) and P=(u:v:w).
Then the 1st barycentric coordinate of 5P-s-Tf3(P) will be:
p P (-Q r + q R) (-2 b2 c2 p P Q r – a2 c2 P q Q r – b2 c2 P q Q r + c4 P q Q r + 2 b2 c2 p P q R + a2 c2 p q Q R + b2 c2 p q Q R – c4 p q Q R + a2 b2 P q r R – b4 P q r R + b2 c2 P q r R – a2 b2 p Q r R + b4 p Q r R – b2 c2 p Q r R) u + (a2 c2 p2 P2 Q2 r2 + b2 c2 p2 P2 Q2 r2 – c4 p2 P2 Q2 r2 + 2 a2 c2 p P2 q Q2 r2 – 2 a2 c2 p2 P2 q Q r R – 2 b2 c2 p2 P2 q Q r R + 2 c4 p2 P2 q Q r R – 2 a2 c2 p P2 q2 Q r R – 2 a2 c2 p2 P q Q2 r R – a4 p P2 q Q r2 R + b4 p P2 q Q r2 R – 2 b2 c2 p P2 q Q r2 R + c4 p P2 q Q r2 R – a4 P2 q2 Q r2 R + a2 b2 P2 q2 Q r2 R – a2 c2 P2 q2 Q r2 R + a4 p2 P Q2 r2 R – b4 p2 P Q2 r2 R + 2 b2 c2 p2 P Q2 r2 R – c4 p2 P Q2 r2 R + a4 p P q Q2 r2 R – a2 b2 p P q Q2 r2 R + a2 c2 p P q Q2 r2 R + a2 c2 p2 P2 q2 R2 + b2 c2 p2 P2 q2 R2 – c4 p2 P2 q2 R2 + 2 a2 c2 p2 P q2 Q R2 + a4 p P2 q2 r R2 – b4 p P2 q2 r R2 + 2 b2 c2 p P2 q2 r R2 – c4 p P2 q2 r R2 – a4 p2 P q Q r R2 + b4 p2 P q Q r R2 – 2 b2 c2 p2 P q Q r R2 + c4 p2 P q Q r R2 + a4 p P q2 Q r R2 – a2 b2 p P q2 Q r R2 + a2 c2 p P q2 Q r R2 – a4 p2 q Q2 r R2 + a2 b2 p2 q Q2 r R2 – a2 c2 p2 q Q2 r R2 + a4 P2 q2 r2 R2 + a2 b2 P2 q2 r2 R2 – a2 c2 P2 q2 r2 R2 – 2 a4 p P q Q r2 R2 – 2 a2 b2 p P q Q r2 R2 + 2 a2 c2 p P q Q r2 R2 + a4 p2 Q2 r2 R2 + a2 b2 p2 Q2 r2 R2 – a2 c2 p2 Q2 r2 R2) v
+ (a2 b2 p2 P2 Q2 r2 – b4 p2 P2 Q2 r2 + b2 c2 p2 P2 Q2 r2 + a4 p P2 q Q2 r2 – b4 p P2 q Q2 r2 + 2 b2 c2 p P2 q Q2 r2 – c4 p P2 q Q2 r2 + a4 P2 q2 Q2 r2 – a2 b2 P2 q2 Q2 r2 + a2 c2 P2 q2 Q2 r2 – 2 a2 b2 p2 P2 q Q r R + 2 b4 p2 P2 q Q r R – 2 b2 c2 p2 P2 q Q r R – a4 p P2 q2 Q r R + b4 p P2 q2 Q r R – 2 b2 c2 p P2 q2 Q r R + c4 p P2 q2 Q r R – a4 p2 P q Q2 r R + b4 p2 P q Q2 r R – 2 b2 c2 p2 P q Q2 r R + c4 p2 P q Q2 r R – 2 a4 p P q2 Q2 r R + 2 a2 b2 p P q2 Q2 r R – 2 a2 c2 p P q2 Q2 r R – 2 a2 b2 p P2 q Q r2 R – a4 P2 q2 Q r2 R – a2 b2 P2 q2 Q r2 R + a2 c2 P2 q2 Q r2 R + 2 a2 b2 p2 P Q2 r2 R + a4 p P q Q2 r2 R + a2 b2 p P q Q2 r2 R – a2 c2 p P q Q2 r2 R + a2 b2 p2 P2 q2 R2 – b4 p2 P2 q2 R2 + b2 c2 p2 P2 q2 R2 + a4 p2 P q2 Q R2 – b4 p2 P q2 Q R2 + 2 b2 c2 p2 P q2 Q R2 – c4 p2 P q2 Q R2 + a4 p2 q2 Q2 R2 – a2 b2 p2 q2 Q2 R2 + a2 c2 p2 q2 Q2 R2 + 2 a2 b2 p P2 q2 r R2 – 2 a2 b2 p2 P q Q r R2 + a4 p P q2 Q r R2 + a2 b2 p P q2 Q r R2 – a2 c2 p P q2 Q r R2 – a4 p2 q Q2 r R2 – a2 b2 p2 q Q2 r R2 + a2 c2 p2 q Q2 r R2) w
Properties
- 5P-s-Tf3(5P-s-P1) = 5P-s-P1.
- 5P-s-Tf3(P) in a 5-Point = the Inverse Scimemi Transformation wrt the 5P-circumscribed conic 5P-s-Co1. See CO-Tf3.
- The locus of QA-Tf6 wrt a pencil of lines through random point P is a circle QA-Tf6a(P). The 5 versions of QA-Tf6a(P) in a 5-Point have as common point 5P-s-Tf3(P).
- 5P-s-Tf3 maps a conic into a conic, also the centers of the conics. See [34], Eckart Schmidt, QFG#2792.
- 5P-s-Tf3 of points P on a line L give the line 5P-s-Tf4(L). See [34], Eckart Schmidt, QFG#2792.
- Pedal points of P on 5P-s-Tf4(L) for lines L through P give a circle with diameter P.Tf3(P). See [34], Eckart Schmidt, QFG#2792.
- Lines P.5P-s-Tf3(P) for points P on a line L give a parabola tangent to L and the axes of 5P-s-Co1. Its directrix is 5P-s-P1.5P-s-Tf3(Q) with Q = pole of L wrt 5P-s-Co1. Its focus is the 2nd intersection of Q.5P-s-P1 and the circumcircle of the triangle with sidelines L and the axes of 5P-s-Co1. See [34], Eckart Schmidt, QFG#2792.
- Lines P.5P-s-Tf3(P) for points P on 5P-s-Co1 give an astroid with the same axes as 5P-s-Co1 and common tangents with 5P-s-Co1 which form a square and cusps inverse to the apexes of 5P-s-Co1 wrt the circumcircle of the square. See [34], Eckart Schmidt, QFG#2792.
Estimated human page views: 321
