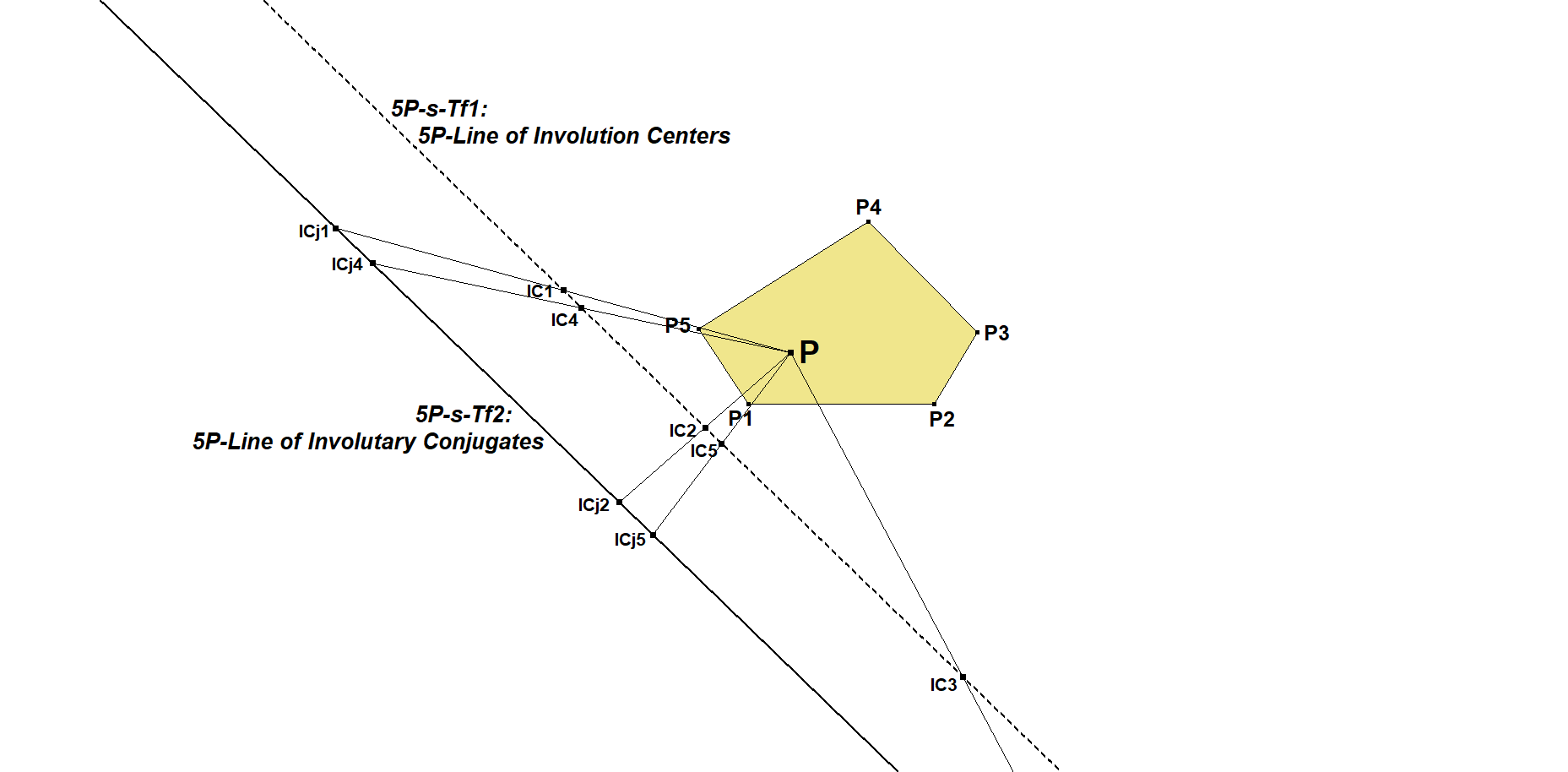
5P-s-Tf2: 5P-Conical Polar / 5P-Line of Involutary Conjugates
5P-s-Tf2 is a transformation that maps some point P into a line of Involutary Conjugates.
Each 5-Point (Pentangle) contains 5 4-Points (Quadrangles).
In a Quadrangle QA-Tf2(P) is the Involutary Conjugate on the tangent line at P to the conic through the vertices of the reference quadrangle and P.
The 5 versions of QA-Tf2(P) are collinear on 5P-s-Tf2(P).
The 5P-Line-of-Involutary-Conjugates of some point P is also the Conical Polar (Co-Tf1) of P wrt the circumscribed conic of the reference 5-Point. See Co-Tf1.
Properties
• When P = 5P-s-P1, then 5P-s-Tf2(P) = Line at Infinity.
• When P lies on the 5P-circumscribed conic 5P-s-Co1, then 5P-s-Tf2(P) is the tangent at P to 5P-s-Co1.
• 5P-s-Tf2(P) is the polar of P wrt the circumscribed conic 5P-s-Co1 and P is the pole of 5P-s-Tf2(P) wrt the circumscribed conic 5P-s-Co1.
• 5P-s-Tf1(P) // 5P-s-Tf2(P).
• d(P,5P-s-Tf1(P)) = d(5P-s-Tf1(P),5P-s-Tf2(P)) = d(P,5P-s-Tf2(P)) / 2.
• P is the Railway Watcher of lines 5P-s-Tf1(P) and 5P-s-Tf1(P). See QL-L-1.
• 5P-s-Tf2 of points P on a line L give a line pencil through the pole of L wrt 5P-s-Co1. See Ref-34, Eckart Schmidt, QFG#2792.
• Parallels to 5P-s-Tf1,2(P) through P for points P on a line L give a parabola. For more information on this parabola see Ref-34, Eckart Schmidt, QFG#2792.
Properties
• When P = 5P-s-P1, then 5P-s-Tf2(P) = Line at Infinity.
• When P lies on the 5P-circumscribed conic 5P-s-Co1, then 5P-s-Tf2(P) is the tangent at P to 5P-s-Co1.
• 5P-s-Tf2(P) is the polar of P wrt the circumscribed conic 5P-s-Co1 and P is the pole of 5P-s-Tf2(P) wrt the circumscribed conic 5P-s-Co1.
• 5P-s-Tf1(P) // 5P-s-Tf2(P).
• d(P,5P-s-Tf1(P)) = d(5P-s-Tf1(P),5P-s-Tf2(P)) = d(P,5P-s-Tf2(P)) / 2.
• P is the Railway Watcher of lines 5P-s-Tf1(P) and 5P-s-Tf1(P). See QL-L-1.
• 5P-s-Tf2 of points P on a line L give a line pencil through the pole of L wrt 5P-s-Co1. See Ref-34, Eckart Schmidt, QFG#2792.
• Parallels to 5P-s-Tf1,2(P) through P for points P on a line L give a parabola. For more information on this parabola see Ref-34, Eckart Schmidt, QFG#2792.