5P-s-P4 5P-Keizer-Schmidt Center
This point was found by Bernard Keizer and Eckart Schmidt searching for the background of 5 mysterious points, being the 5 common points of the 3 QL-versions of the cubic QA-Cu7.
See [34], QFG#3256.
Construction
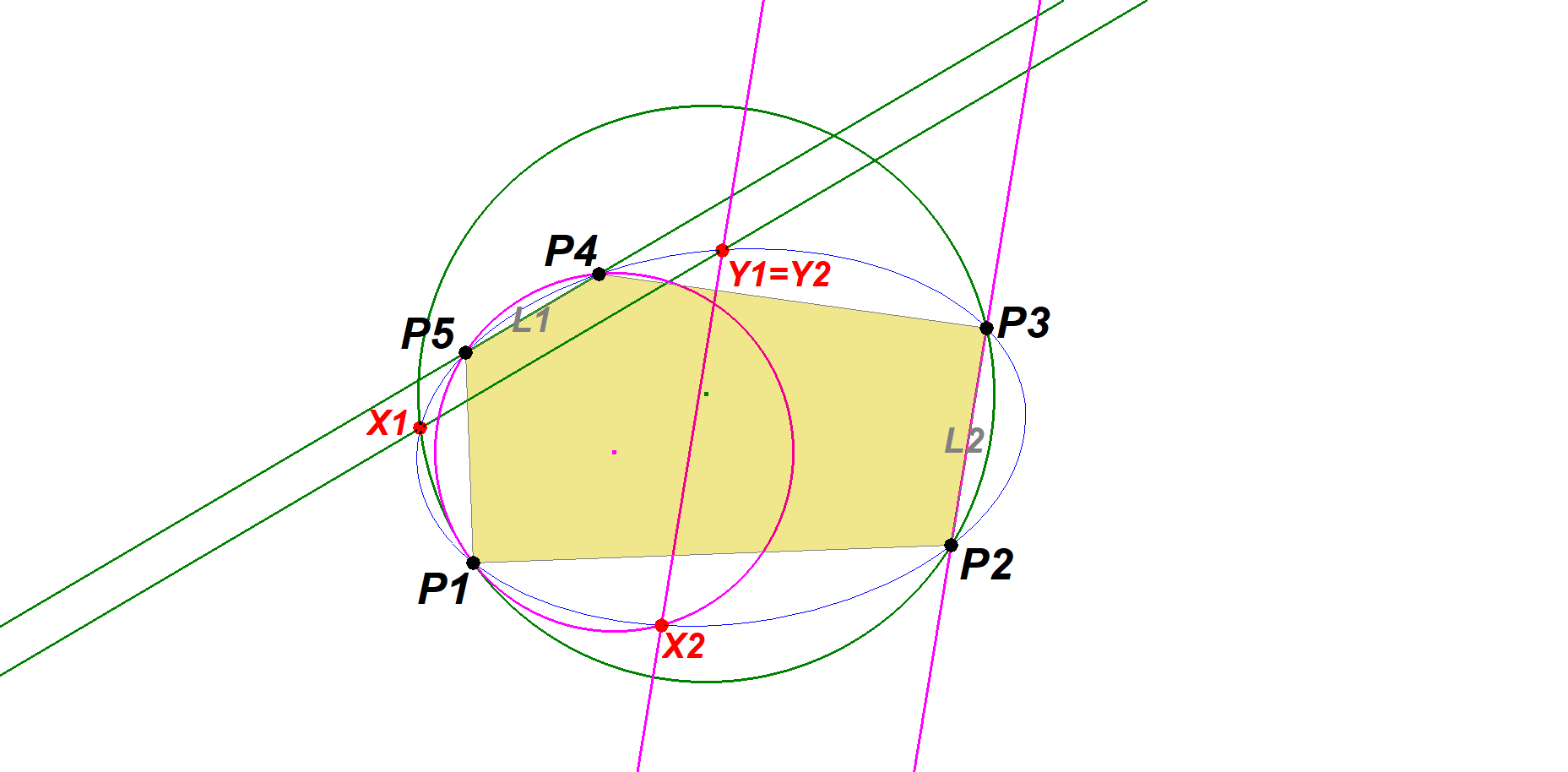
Consider a 5P with circumconic Co
… and a line L connecting two 5P-vertices
… and the circumcircle Ci of the remaining vertices.
… Let X be the 4th intersection of Ci and Co,
… let L’ be a parallel to L through X,
… intersecting Co further in Y,
… which will be a new 5P-point on the circumconic,
… independent of the choice of vertices.
Coordinates
When using barycentric coordinates: P1=(1:0:0), P2=(0:1:0), P3=(0:0:1), P4=(p:q:r), P5=(P:Q:R),
then 5P-s-P4 has coordinates:
(p P/Ta : q Q/Tb : r R/Tc),
where:
Ta = +c2 p P2 q-c2 p2 P Q+b2 p P2 r+a2 P2 q r+b2 p P Q r-c2 p P Q r+a2 P q Q r
-b2 p2 P R-b2 p P q R+c2 p P q R-a2 p2 Q R-a2 p q Q R+a2 P q r R-a2 p Q r R,
Tb = -c2 P q2 Q+c2 p q Q2+b2 p P Q r+a2 P q Q r-c2 P q Q r+b2 p Q2 r+a2 q Q2 r
-b2 p P q R-b2 P q2 R-a2 p q Q R+c2 p q Q R-a2 q2 Q R-b2 P q r R+b2 p Q r R,
Tc = -c2 p P Q r-c2 P q Q r-c2 P Q r2+c2 p P q R+c2 p q Q R+a2 P q r R-b2 P q r R
-a2 p Q r R+b2 p Q r R-b2 P r2 R-a2 Q r2 R+c2 p q R2+b2 p r R2+a2 q r R2
Application in Quadrilateral Geometry
A new Quadrangle Transformation QA-Tfx can be made, which considers the reference points of the Quadrangle and a random point P as the 5P (Pentangle) delivering the new 5P-point 5P-s-P4.
Properties of this Quadrangle Transformation QA-Tfx are:
- QA-Tfx (QA-P4) = QA-P1.QA-P42 ^ QA-P3.QA-P4 ^ QA-P6.QA-P34.
- QA-Tfx (QA-P41) lies on QA-P3.QA-P41.
- For a point P on QA-Co3 the image QA-Tfx(P) lies diametral on QA-Co3. See [34], QFG-message #3256 and #3424.
Properties
- In a Triangle 5P-s-P4 of Pentangle ABCBr1Br2 (where Br1, Br2 are the 2 Brocard Points of Triangle ABC) is ETC Center X(99). See [12].
- In a Reference Quadrilateral we have 3 Component Quadrigons (see QL-3QG1). For each Component Quadrigon we can construct the circular cubic QA-Cu1. These three cubics have 5 common points, which form a Pentangle extensively discussed in the Quadri-Figures Group, see [34], keywords “3 QL-versions of QA-Cu7” and “5P-Geometry”. The point 5P-s-P4 of this Pentangle coincides a point T, being the intersection point of the 3 QL-versions of QA-Px.QG-P1 of the Reference Quadrilateral, where QA-Px = QA-P41.QG-P19 ^ QA-P4.QG-P18.
Estimated human page views: 278
