5P-s-Co1 5P-Circumscribed Conic
It is well known that in a system of 5 random Points a unique circumscribed conic can be constructed. This conic is 5P-s-Co1 and its center is 5P-s-P1.
Construction
See Ref-19.
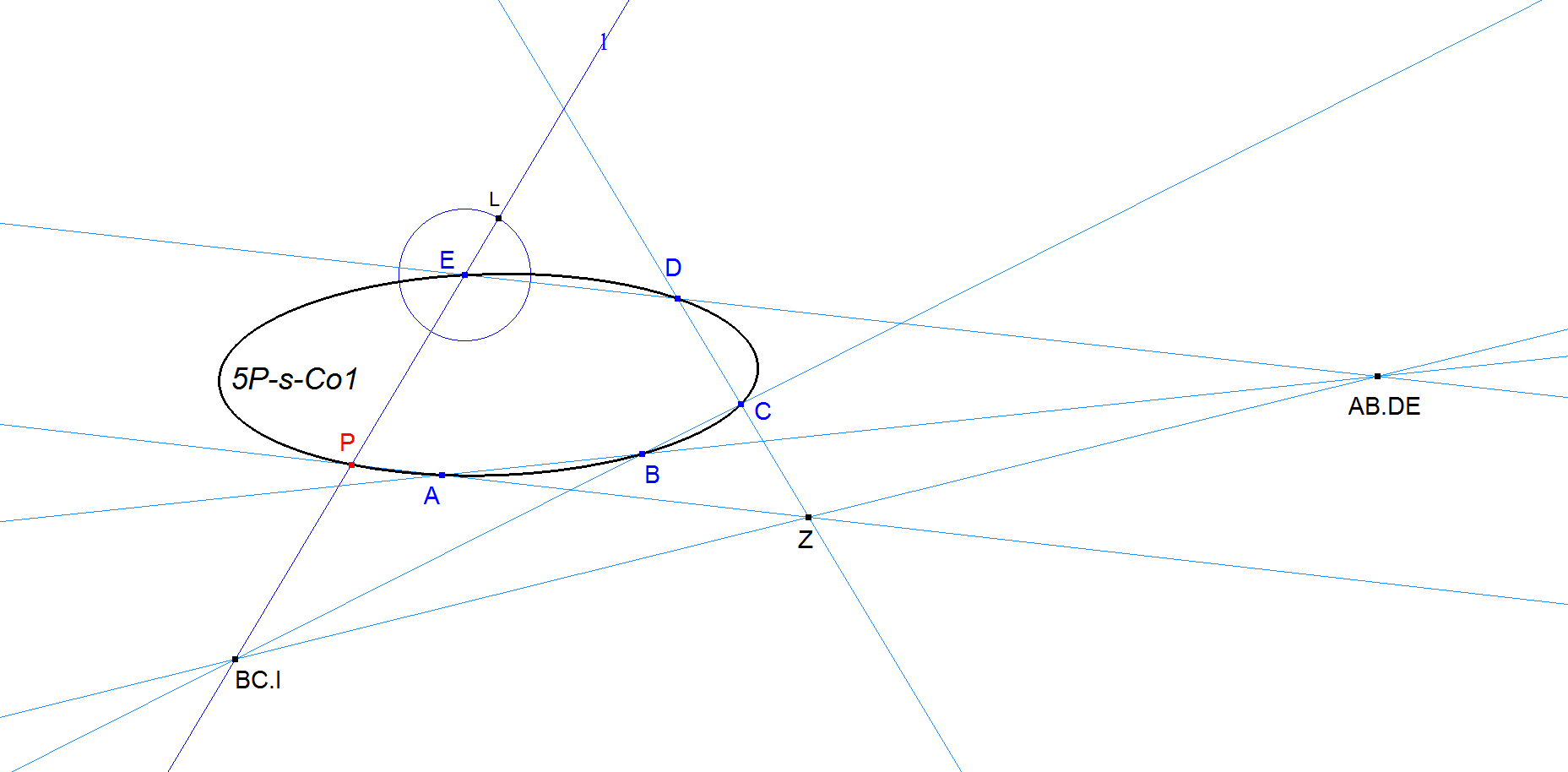
Given five points A, B, C, D, E.
Let l be a variable line through E. (Draw a circle center E with any radius. Let L be an arbitrary point on the circle, and take l to be the line EL.)
The line joining AB.DE and BC.l cuts CD in Z, then P = AZ.l lies on the conic.
As L moves round the circle, P traces the conic. (Select L and P, and Construct/Locus.)
Estimated human page views: 305
