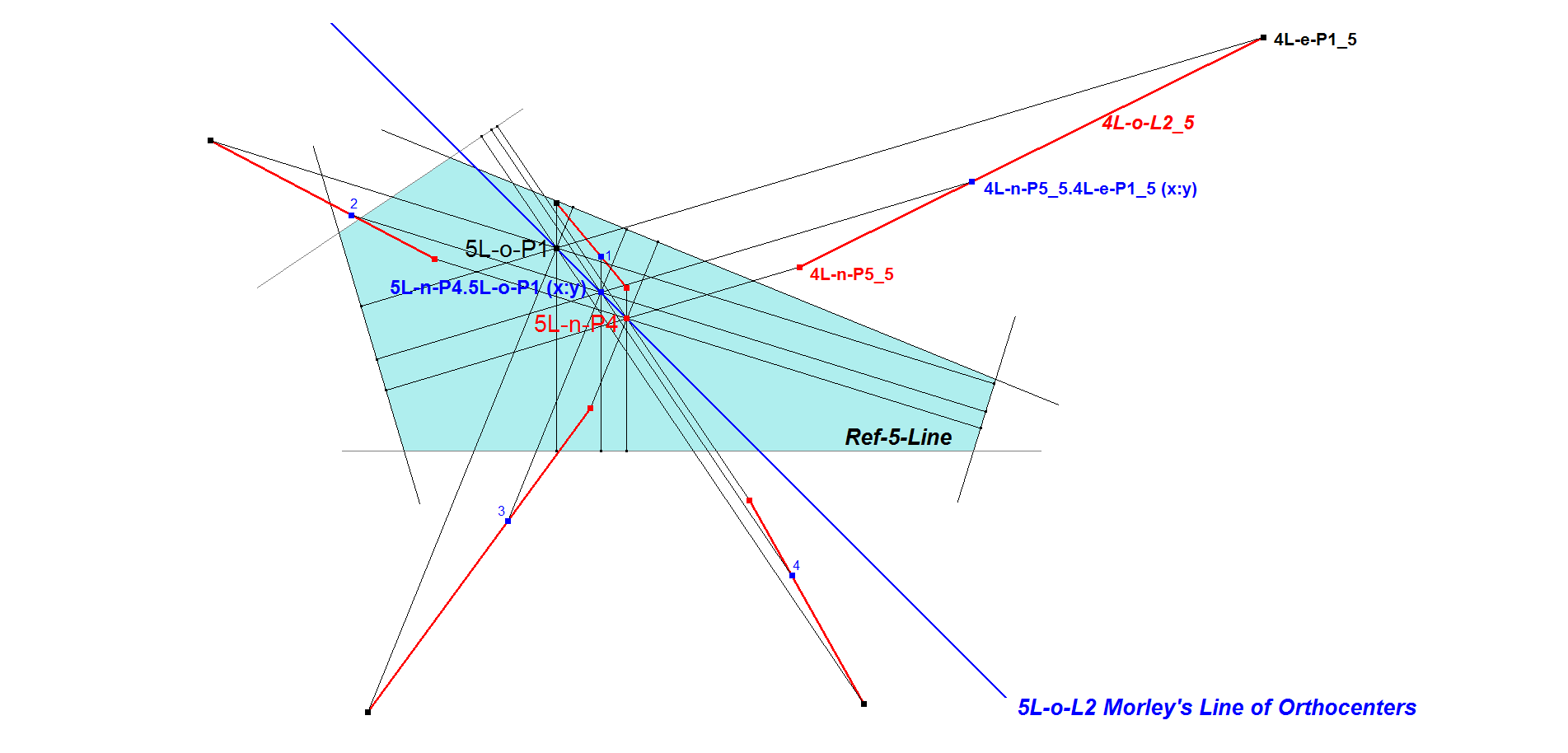
nL-o-L2: nL-Morley’s Line of Orthocenters
Morley describes this line in his paper: Orthocentric properties of the Plane n-line (Ref-49).
It is the line connecting nL-o-P1 (Morley’s 1st Orthocenter) and nL-n-P4 (Morley’s 2nd Orthocenter).
Let X be some point on (n-1)L-e-L2 with fixed ratio wrt (n-1)L-n-P5 and (n-1)L-e-P1. Then nL-o-L2 is the locus of the common intersection point of the perpendiculars through the n lower level versions of X to the omitted line (Level-up Construction nL-n-Luc1) preserving distance ratios.
In this way (n-1)L-e-P1 is transformed into nL-o-P1 and (n-1)L-n-P5 is transformed into nL-n-P4.
Correspondence with ETC/EQF
- When n=3, then 3L-o-L2 = X(4).X(4) = undefined line.
Properties
- These points lie on nL-o-L2 (all Orthocenters indeed):
- nL-o-P1 (nL-Morley’s 1st Orthocenter
- nL-n-P4 (nL-Morley’s 2nd Orthocenter)
- nL-n-P10 (nL-MVP Orthocenter)
Estimated human page views: 325
