nL-o-L1: nL-Line of Inscribed EnnaDeltoid Centers
Morley describes this line in his paper: Orthocentric properties of the Plane n-line (Ref-49).
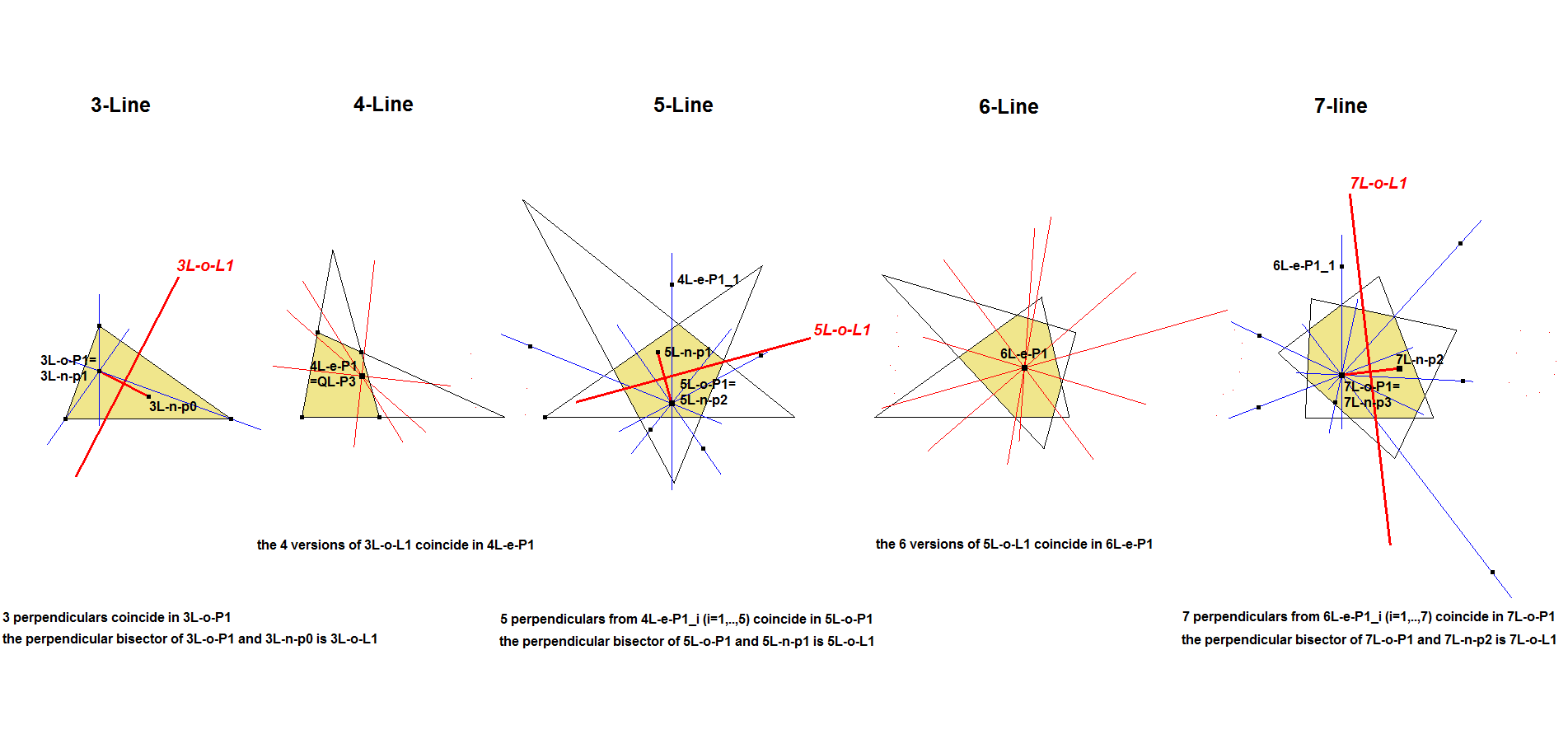
It is the locus of all (n+1)L-e-Cv1 centers ((n+1)L-e-P1) and is always a line (Theorem 8) for all odd n. The (n+1)-Line is constructed by adding a random line to the reference n-Line. Every added line contributes a point on nL-o-L1.
nL-o-L1 is the Perpendicular Bisector of nL-n-p((n-3)/2).nL-n-p((n-1)/2). Note that the letter “p” is in lower case. See nL-n-pi.
For example in a 5-Line it is the perpendicular bisector of 5L-n-p1. 5L-n-p2 and in a 7-Line it is the perpendicular bisector of 5L-n-p2. 5L-n-p3.
The merit of nL-o-L1 is that in an (n+1)-Line the n versions of nL-o-L1 concur in (n+1)L-e-P1 being nL-Morley’s EnnaDeltoid Center.
Correspondence with ETC/EQF
- When n=3, then nL-o-L1 = Perpendicular Bisector of line segment X(3).X(4).
- When n=4, then the 4 versions of 3L-o-L1 = Perpendicular Bisector of line segment X(3).X(4) concur in 4L-e-P1, which is QL-P3.
Estimated human page views: 286
