nL-o-2L1: nL-Orthogonal Reflective Axes
There are n versions of (n-1)-Lines contained in an n-Line.
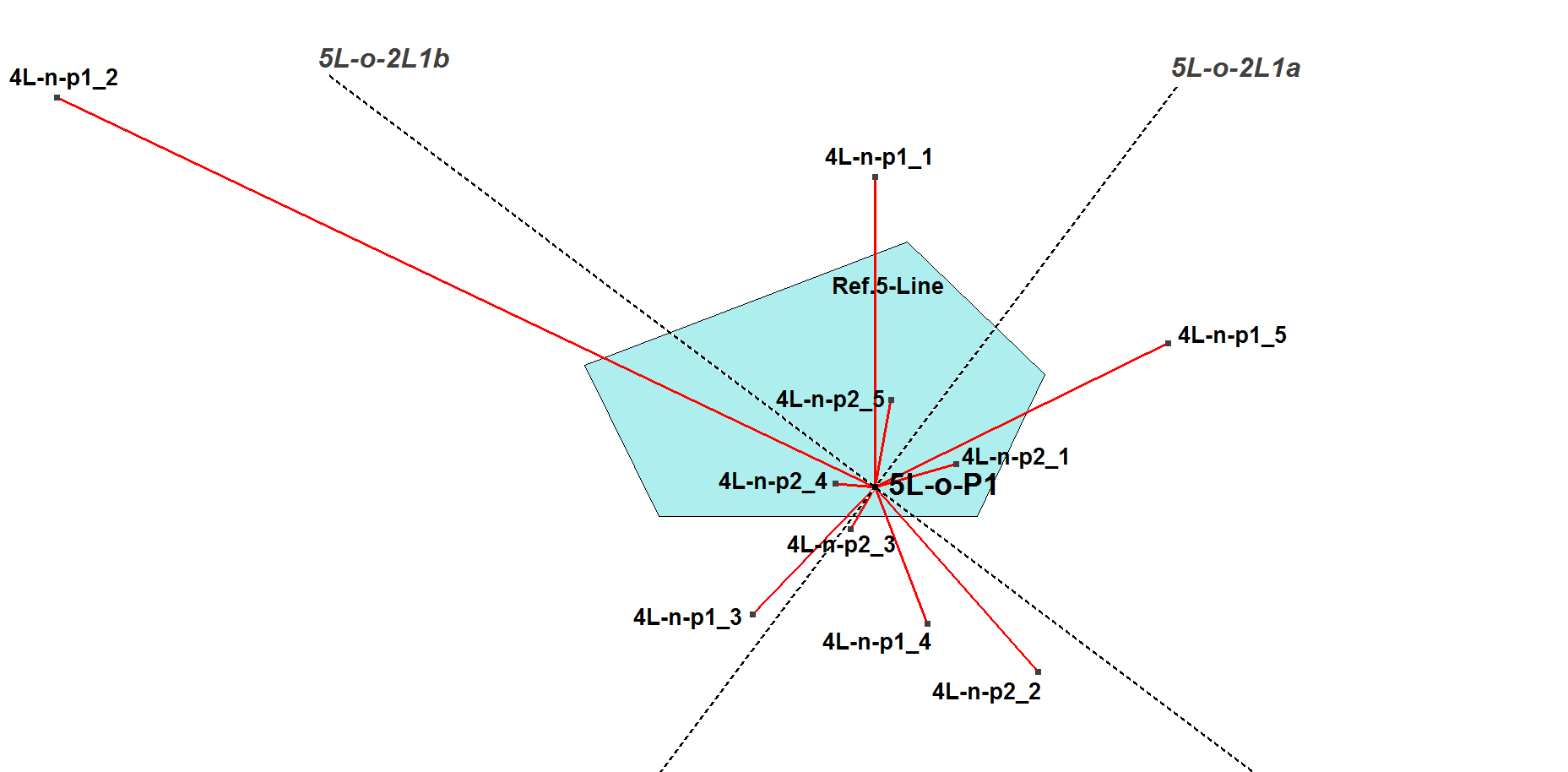
For n=odd there are two orthogonal axes (nL-o-2L1) at Morley’s first Orthocenter X=nL-o-P1 being the common angle bisectors of the n versions of angles mL-n-ph.X.mL-n-pk, where m=(n-1), h=(n-1)/2, k=(n-3)/2. Note that the letter “p” is in lower case. See nL-n-pi for definition of these points.
Moreover the distance ratios X.mL-n-ph_i / X.mL-n-pk_i are equal for i=1, … ,n.
The Reflective Axes exist for n=5,7,9,…. (not for n=3).
See nL-o-P1. See also [34], QFG-message #910.
Example:
5L-o-2L1a/b are the common angle bisectors of the 5 versions of angles 4L-n-p2_i.X.4L-n-p1_i (where X=5L-o-P1) and the distance ratios X.4L-n-p2_i / X.4L-n-p1_i are equal for i=1, … ,5.
Correspondence with ETC/EQF
- When n=3, then 3L-o-2L1 is not defined.
Estimated human page views: 314
