nL-n-Tf3 nL-2nd Generation nL-Orthopole
Let L be a random line.
Let nLL be the 2nd generation n-Line made up from the n versions of (n-1)L-n-Tf2(L).
The 3rd generation n-Line constructed in a similar way upon nLL are n coinciding Lines, being nL-n-Tf4(L). The lines L, nL-n-Tf2(L), nL-n-Tf4(L) coincide in one point being nL-n-Tf3(L).
5-Line Example
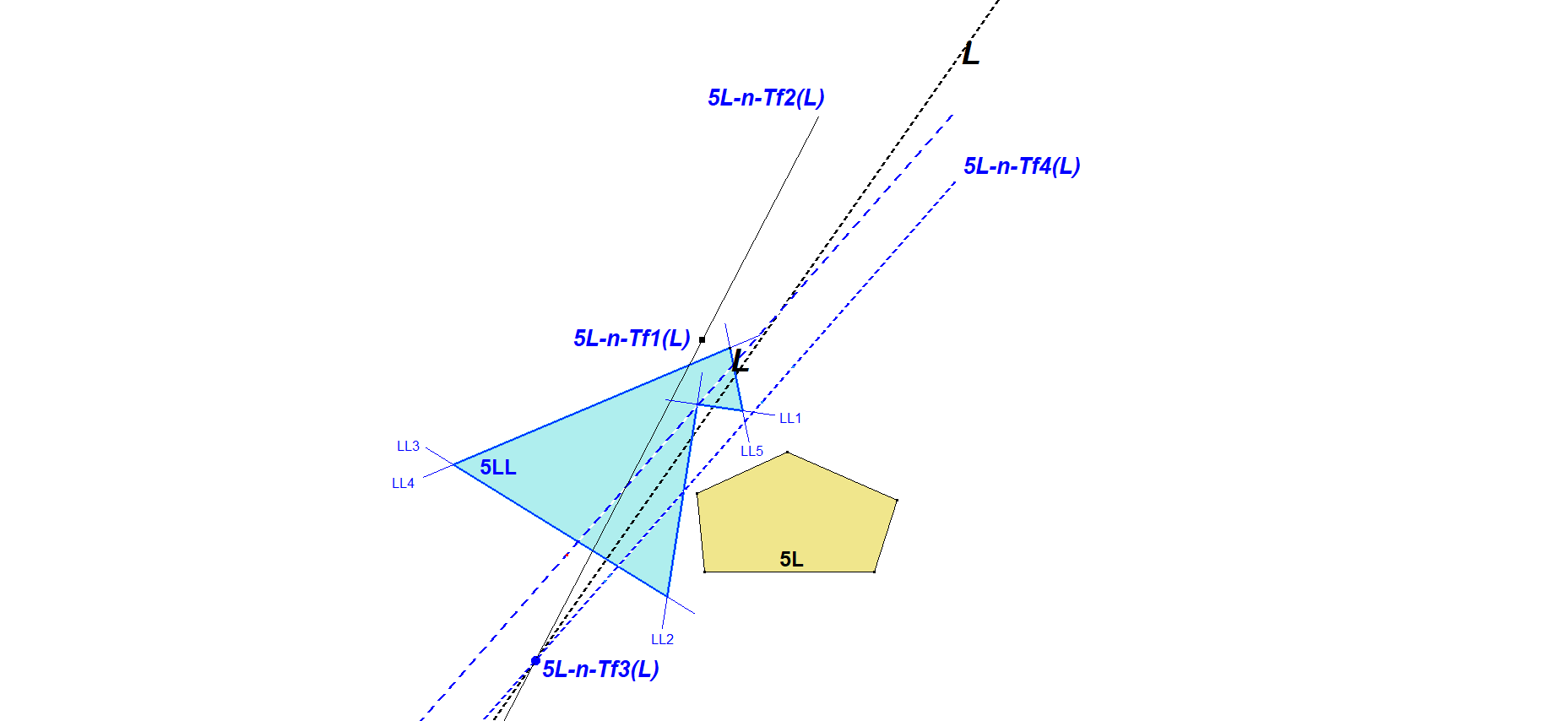
The 2nd Generation nL-Orthopolar best can be understood by the example in a 5-Line.
The 5 versions of 4L-n-Tf2(L) form the 2nd generation Orthopolar 5-Line, being called here 5LL.
The 5 versions of 4L-n-Tf2(L) wrt 5LL delivers 5 times the same line, which is 5L-n-Tf4(L).
The lines L, 5L-n-Tf2(L), 5L-n-Tf4(L) coincide in one point being 5L-n-Tf3(L).
Notes
- Note that for all L the sides of 5LL have a fixed direction regardless the position of L.
- Note that for all L in the same direction corresponding 5LL’s are congruent.
Properties
- Let nLL-n-Tf2(L) be nL-n-Tf2(L) wrt nLL.
- nLL-n-Tf2 has some very special properties:
- nLL-n-Tf2(La) // nLL-n-Tf2(Lb), where La and Lb are two different random lines.
- nLL-n-Tf2(L) will be a line passing through the intersection point of L and nL-n-Tf2(L).
- the n versions of (n-1)LL-n-Tf2(LLi) coincide with a line // nLL-n-Tf2(L), where LLi is the omitted line of nLL and i=1, …, n.
- the n versions of (n-1)LL-n-Tf2(L) coincide with nLL-n-Tf2(L).
Estimated human page views: 327
