nL-n-Tf1 nL-Orthopole
nL-n-Tf1 is the generalization of the Orthopole in a triangle.
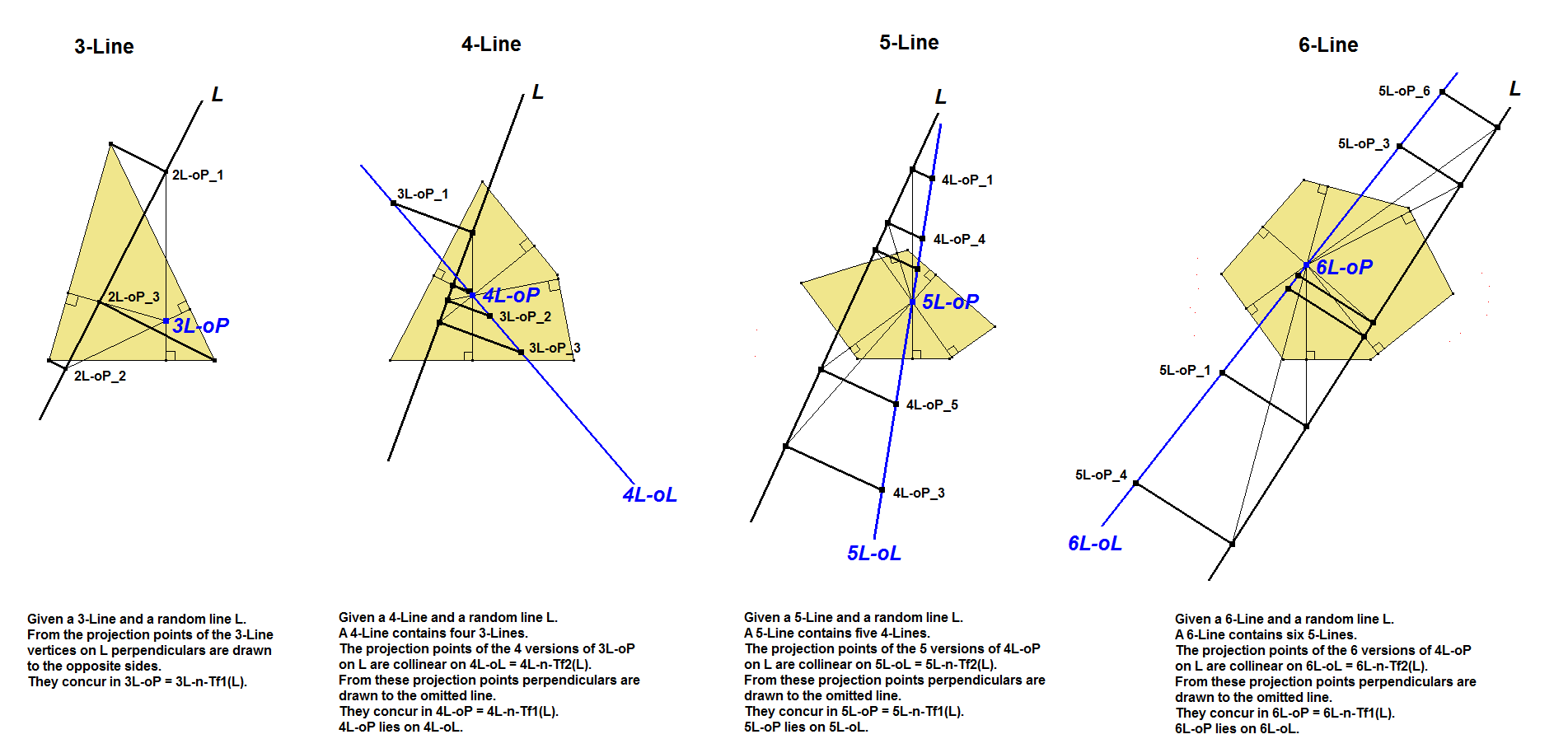
nL-n-Tf1 is the transformation which transforms a random line L into an “nL-Orthopole”, which is a point in an n-Line.
In a 3-Line it is the well-known Orthopole in a Triangle. See Ref-13.
In a 4-Line it is the Orthopole in a Quadrilateral which was introduced by Tran Quang Hung. See [34], QFG#2062, #2064, #2069, #2070.
The method for constructing an Orthopole in an n-Line can be made recursive by using the same method. See figure below. See [34], QFG#2086.
Properties
- An n-Line contains n (n-1)-Lines. The n versions of the (n-1)L-Orthopole in an n-Line will be collinear on the line nL-n-Tf2(L), whilst nL-n-Tf1(L) will be lying on nL-n-Tf2(L).
- An (n+1)-Line contains (n+1) n-Lines. The (n+1) versions of the nL-Orthopole in an (n+1)-Line will be collinear. See nL-n-Tf2.
Estimated human page views: 306
