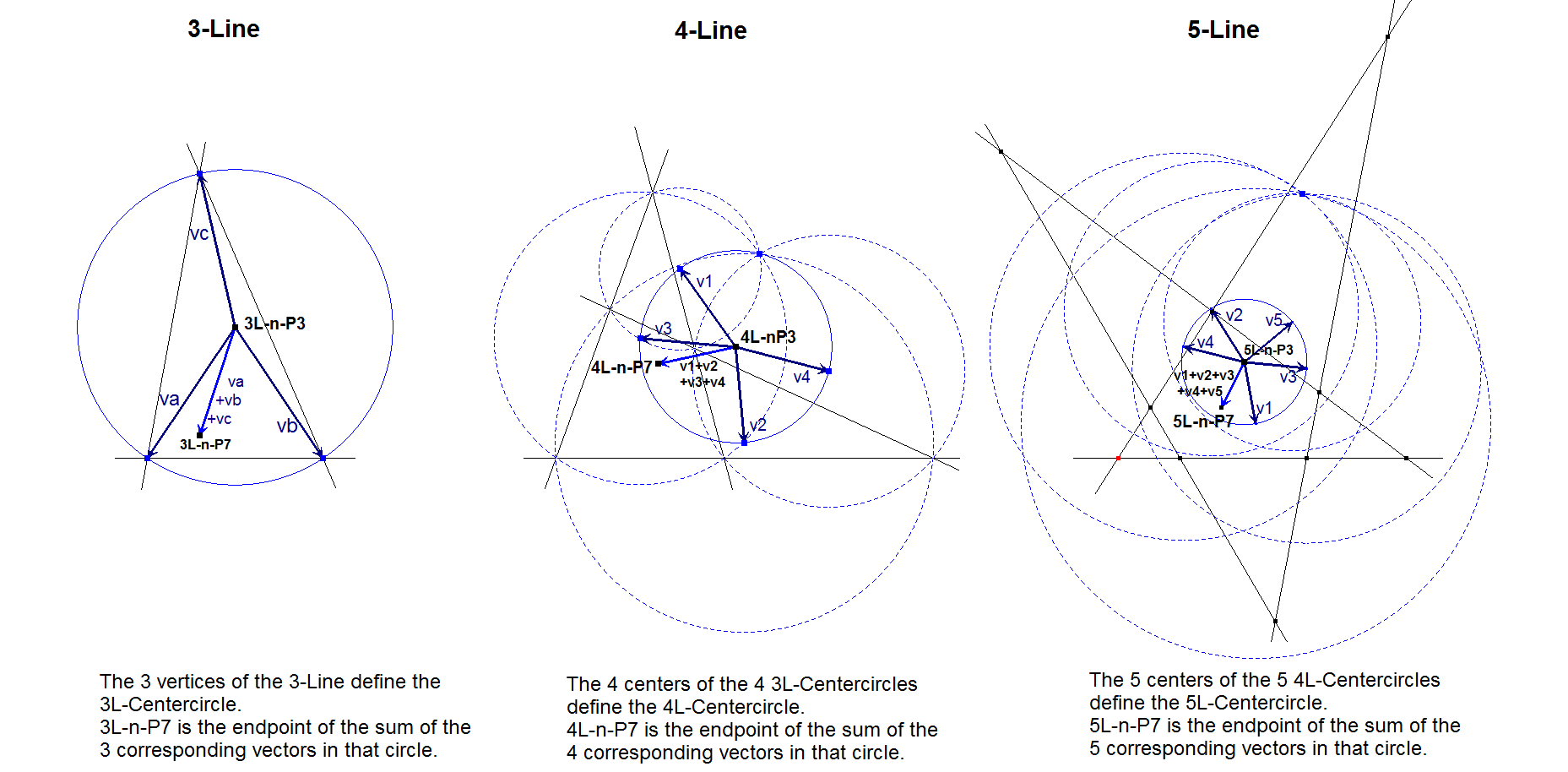
nL-n-P7: nL-Hervey Point
The Hervey Point is defined by Morley as the endpoint of the sum of n vectors (Level-up Construction nL-n-Luc3) with common origin nL-n-P3 and endpoints the n (concyclic) lower level points (n-1)L-n-P3.
Goormaghtigh describes this n-Line point in Ref-55 referring to Morley’s document Ref-49 and calls it the Hervey Point, because in a Quadrilateral this point coincides with a point earlier described by Hervey (QL-P3).
Morley describes in Ref-49 some recursive intermediate points “pi“ for i=0, .. , n/2 (see nL-n-pi) that are useful for constructing other points. In this notation nL-n-P7 = p1 (or in EPG notation: nL-n-p1).
Correspondence with ETC/EQF
Properties
- The ratio d(nL-n-P7, (n-1)L-n-P3) : d(nL-n-P7, (n-1)L-n-P7) is fixed for all n Component m-Lines, where m=(n-1). According to Goormaghtigh (see Ref-55) this ratio = Radius-of-Centercircle : d(nL-n-P1,nL-n-P3).
- In a 5-Line construct the 5 versions of QL-L4 (Morley Line) in each Component 4-Line. They form the 1st generation Morley 5-Line. Do the same process in the 1st generation Morley 5-Line. This leads to the 2nd generation Morley 5-Line consisting of 5 lines concurring in 5L-n-P7. This point is also the common point QL-P3 of all Component 4-Lines of the 1st generation Morley 5-Line. See [34], QFG # 826.
- In a 6-Line the six 5L-versions of 5L-n-P7 are coconic.
Estimated human page views: 313
