nL-n-P12: nL-QL-P4 Par1/Par2-Homothetic Center
nL-n-P12 is the Par1/Par2-Homothetic Center (nL-n-Luc5e) of mL-n-P12, where m=(n-1).
This recursive construction can be rolled up to increasing larger values of n.
Starting value for n is 4, where 4L-n-P12=QL-P4.
General remarks
With reservations nL-n-P12, nL-n-P13, nL-n-P14 are mentioned as n-points in the neos-system (see nL-1). There are no contra-indications and all Mathematica calculations with numeric examples until reasonable depth confirm they are recursive n-points indeed, however there is no synthetic proof of it yet. So they are mentioned as n-points because their existence is a fact (to a certain n-level) and therefore they deserve registration.
nL-n-P12, nL-n-P13, nL-n-P14 have starting points at n=4, where they represent QL-P4, QL-P28, QL-P29, which are centers related to Hofstadter points, resp. H(2)=X(3), H(3)=X(186), H(-2)=X(265).
Probably there will be corresponding nL-n-points for centers related to other Hofstadter points H(i).
Construction
The construction of nL-n-P12 is as follows.
- Every n-Line contains n (n-1)-Lines leaving one line being called the omitted line.
- Construct lines through the n versions of (n-1)L-n-P12 parallel to the omitted line.
- These n lines form a new n-Line being called Par1.
- In the same way a 2nd generation n-Line Par2 can be constructed.
- Par1 is homothetic to Par2 and so there will be a Homothetic Center, which is nL-n-P12.
- This recursive construction can be rolled up to increasing larger values of n. Starting value for n is 4, where 4L-n-P12=QL-P4.
In a corresponding way nL-n-P13 and nL-n-P14 are constructed.
Example in a 5-Line
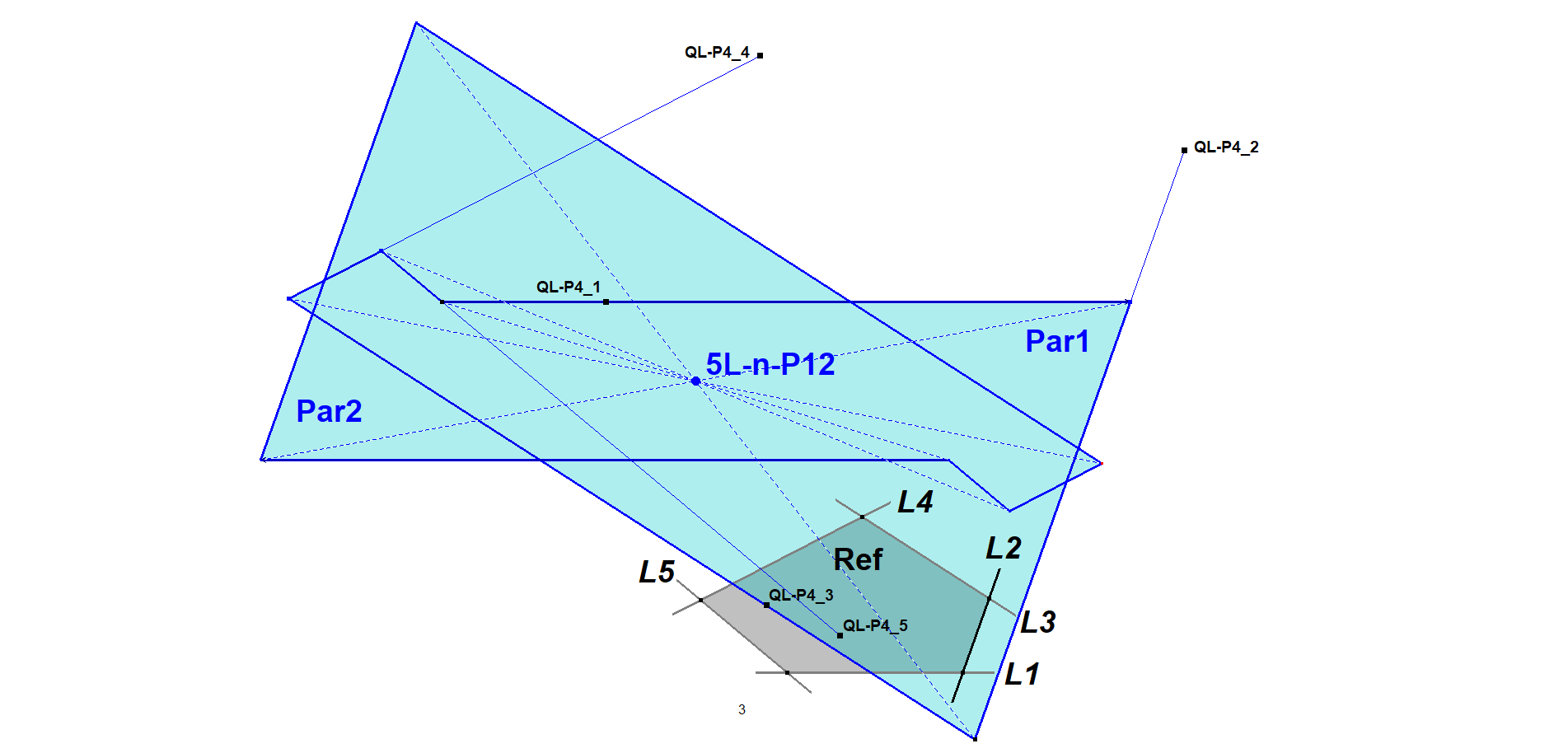
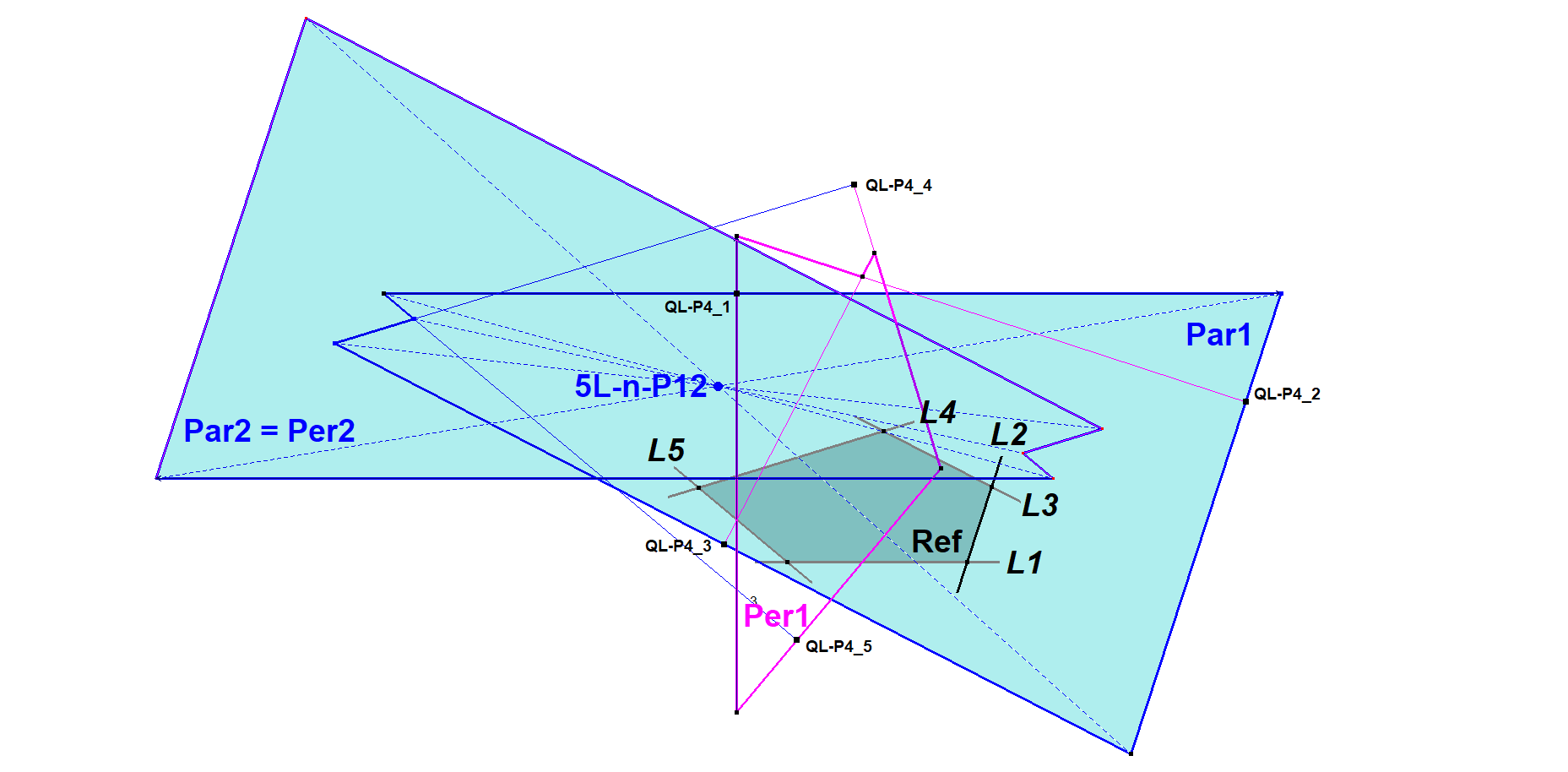
5L-n-P12 is also the Par1/Per2-Homothetic Center (see nL-n-Luc5g) of QL-P4 wrt the Reference 5-Line, because Par2 coincides with Per2.
Correspondence with ETC/EQF
- In a 3-Line:
- Any 3L-Par1/Par2-predecessor ?
- In a 4-Line:
Properties
- In a 5-Line 5L-n-P12 = Midpoint (5L-n-P7.5L-n-P3).
- In a 5-Line 5L-n-P14 = 5L-n-P7. 5L-n-P5 (2:-1)
- It looks like that for all n Par2 will coincide with Per2.
- It looks like that for all n the lengths of the line segments of Par1 are equal to the corresponding line segments of Par2 as well as Per2.
Estimated human page views: 363
