nL-n-Cv1: Morley’s Mono EnnaCardioid
nL-n-iCv1: Morley’s Multiple EnnaCardioids
nL-n-Cv1 and nL-n-iCv1 are curves described by Morley in Ref-37 and Ref-47, with the notation Cn.
The name EnnaCardioid is a generic name introduced by Morley in Ref-47, On Reflexive Geometry, page 15. The names Cardioid, TetraCardioid and PentaCardioid are also used by him.
- In a 3-Line it is a circle (Morley Code C2).
- In a 4-Line it is a regular Cardioid (Morley Code C3).
- In a 5-line it is called a TetraCardioid (Morley code C4).
- In a 6-line it is called a PentaCardioid (Morley code C5).
- etc.
Morley’s pupil Edward C. Philips wrote a dissertation (Ref-56) “On the PentaCardioid” in 1908. In this paper he gives a general description of the different types of PentaCardioids that occur as well as a method of constructing the PentaCardioid.
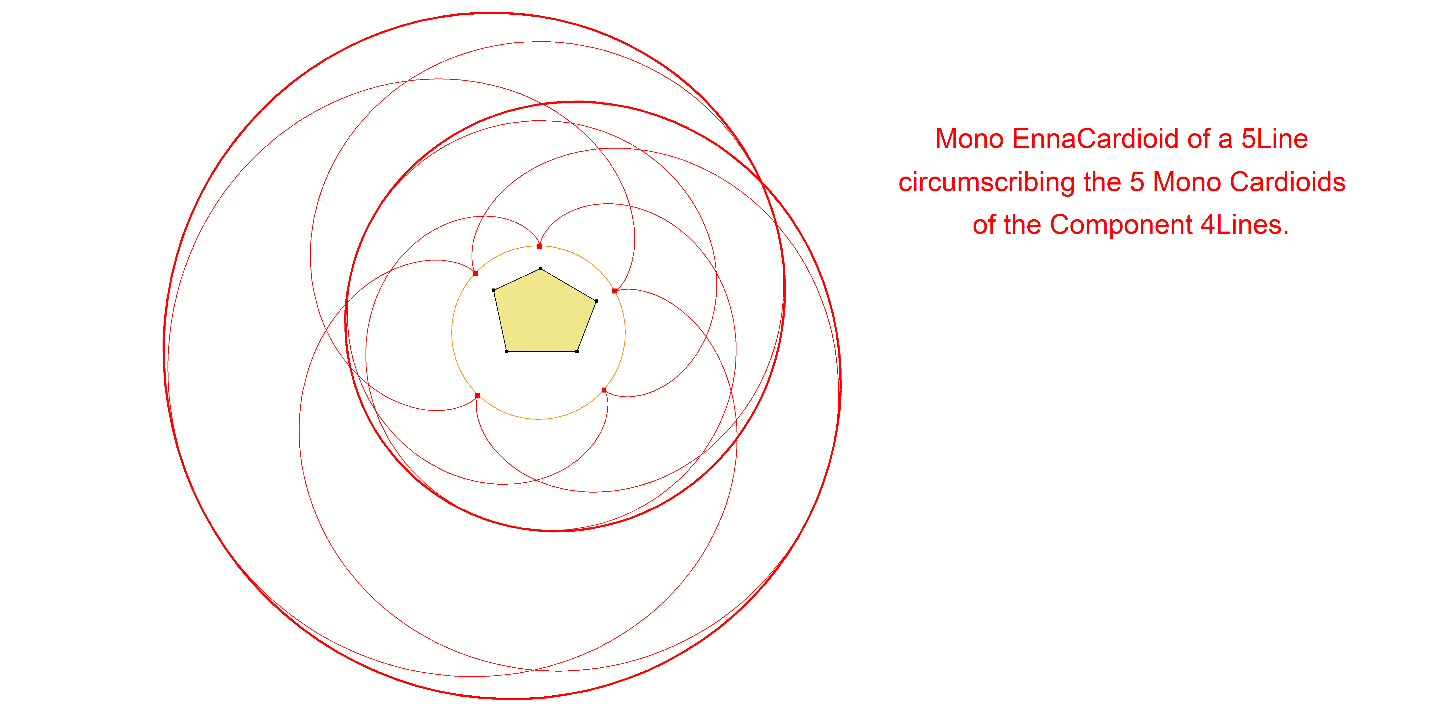
Each nL-Mono EnnaCardioid nL-n-Cv1 is circumscribing n lower-level (n-1)L-EnnaCardioids.
All nL-Multiple EnnaCardioids nL-n-iCv1 are inscribed in the corresponding n-Line and their centers lie on Morley’s Axes nL-n-iL1.
When n=4 it is a regular Cardioid. At higher levels it is a special type of curve often with many cusps.
See also QFG messages #815-#825, #831.
Mono EnnaCardioids and Multiple EnnaCardioids
- In a 3-Line there are:
- 1 Mono Circle C2 here coded 3L-n-Cv1 (circumcircle),
- 4 (=22) Multiple Circles C2 here coded 3L-n-4Cv1 (in-/excircles) touching the defining 3 lines of the 3-Line.
- In a 4-Line there are:
- In a 5-Line there are:
- 1 Mono TetraCardioid C4 here coded 5L-n-Cv1 circumscribing the Mono Cardioids C3 of the 5 Component 4-Lines of the 5-Line,
- 44 Multiple TetraCardioids C4 here coded 5L-n-64Cv1 touching the defining 5 lines of the 5-Line.
- In a 6-Line there are:
- 1 Mono PentaCardioid C5 here coded 6L-n-Cv1 circumscribing the Mono TetraCardioids C4 of the 6 Component 5-Lines of the 6-Line,
- 55 Multiple PentaCardioids C5 here coded 6L-n-3125Cv1 touching the defining 6 lines of the 6-Line.
- etc.
Construction
- For a construction of Morley’s Mono Cardiod in a 4-Line see EQF, QL-Qu1.
- For a construction of Morley’s Multiple Cardiods in a 4-Line see EQF, QL-27Qu1.
Construction of 5L-n-Cv1
(example in a 5-Line by Eckart Schmidt, see QFG#815)
- Let Q be a variable point on the 5L-n-Ci1-circle,
- let Ci1 be a circle round Q through 5L-n-P1,
- let X be the second intersection of Ci1 and the QL-P1-circle,
- let Y be the second intersection of X.5L-o-P2 and Ci1,
- let Ci2 be a circle round Y through X,
- let Z be the second intersection of Ci1 and Ci2,
- then Z reflected in Y is a point P of Morley’s EnnaCardioid.
Correspondence with ETC/EQF
- When n=3, then nL-n-Cv1 = circumcircle of the 3-Line.
- When n=3, then nL-n-iCv1 = combination of incircle and excircles of the 3-Line.
- When n=4, then nL-n-Cv1 = QL-Qu1.
- When n=4, then nL-n-iCv1 = QL-27Qu1.
Estimated human page views: 504
