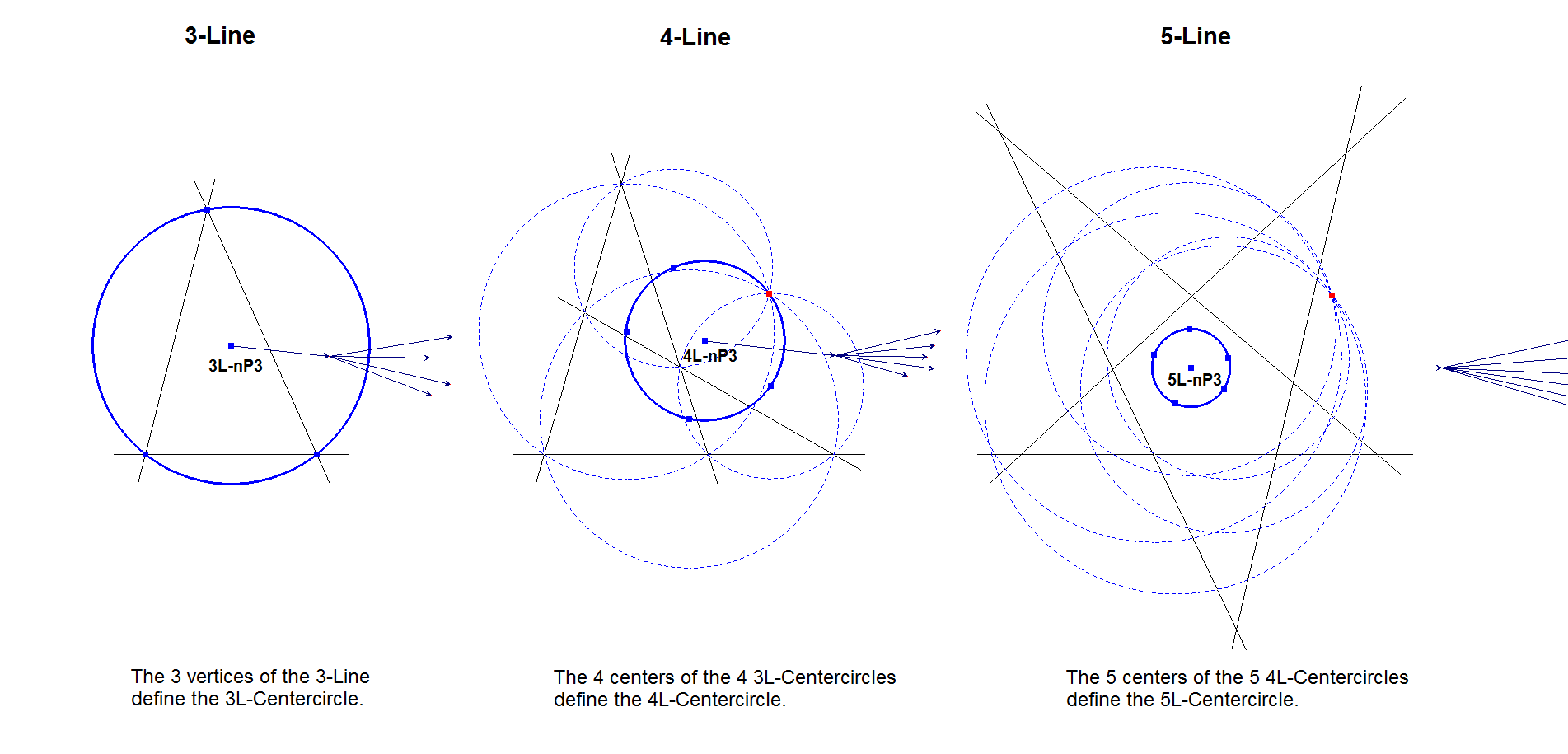
nL-n-Ci1: nL-Center Circle
A Triangle (3-Line) has a circumcircle. Morley in Ref-49 calls this circle a Centercircle.
In a Quadrilateral (4-Line) there are 4 component 3-Lines whose 3L-Centercircle Centers are concyclic on the 4L-Centercircle.
In a Pentalateral (5-Line) there are 5 component 4-Lines whose 4L-Centercircle Centers are concyclic on the 5L-Centercircle. Etc.
Morley proved in Ref-49 that there exists a Centercircle in an n-Line for all n, built from the centers of the Centercircles from the Component m-Lines.
The Center of this Centercircle is nL-n-P3.
Correspondence with ETC/EQF
- When n=3, then nL-n-Ci1 = Triangle Circumcircle.
- When n=4, then nL-n-Ci1 = Miquel Circle QL-Ci3.
- When n=5, then nL-n-Ci1 = Circumcircle of the concyclic five versions of QL-P4.
Properties
- Each Oi.Oj-intercepted inscribed nL-n-Ci1-angle = Angle(Li,Lj) mod π,
- where (i,j) are different numbers from (1, … ,n).
- Note that intercepted inscribed angles in a circle are twofold: α and π – α.
- When taken mod π the angles are α and -α. Anyway the circle is the locus of points which form inscribed angles (mod π) with a line segment, +α when occurring on one side of the line segment and -α when occurring on the other side.
- The same is true for angles between two intersecting lines. They are twofold and when taken mod π they are +α and -α.
- Example: let V be variable point on nL-n-Ci1, now the twofold angle Oi.V.Oj = twofold angle (Li,Lj). See [34], QFG#1893.
Estimated human page views: 338
