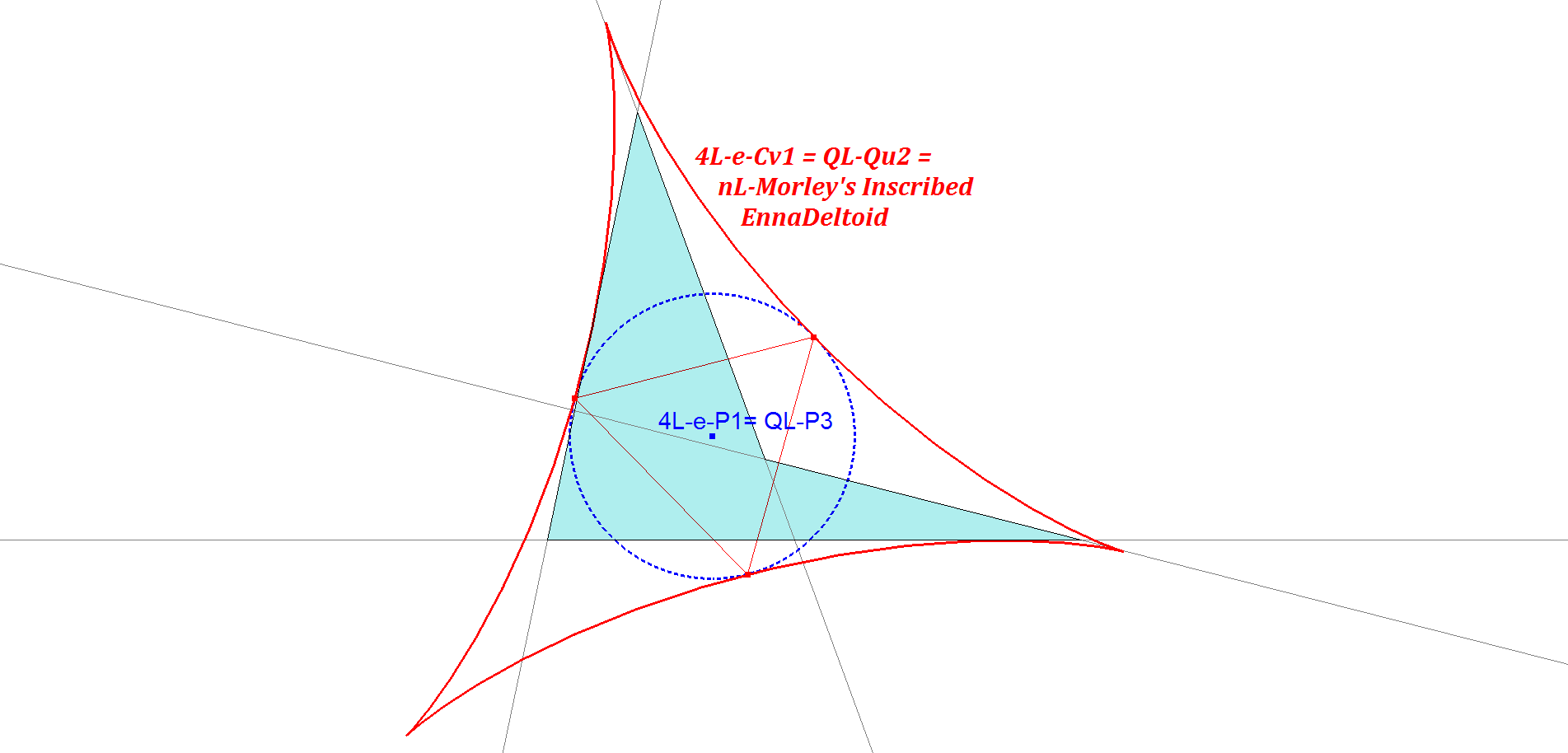
nL-e-Cv1: nL-Morley’s Inscribed EnnaDeltoid
Morley describes “The Deltoid” in his paper: Orthocentric properties of the Plane n-line (Ref-49).
He writes at page 7: “The peculiar appropriateness of the deltoid for the metrical theory of four lines makes it desirable to have an analogous curve for 2n-lines”. This curve is called Δ2n-1.
Then: “Theorem 6: there are 2n-1 cusp-tangents of Δ2n-1; they touch a concentric Δ2n-3.”
Important is that he shows that the inscribed deltoid in a 4-Line is the prelude for similar curves at higher even levels.
Similar to the Cardioids (see nL-nCv1) the higher level deltoids will be named here EnnaDeltoids.
It is not quite clear yet how the EnnaDeltoids looks like for n>4.
According to Morley the center of the EnnaDeltoid’s is nL-e-P1.
Correspondence with ETC/EQF
- When n=4, then nL-e-Cv1 = QL-Qu2 (Kantor-Hervey Deltoid).
Estimated human page views: 279
