6L-s-Tf1 6L-Schmidt Transformation
6L-s-Tf1 was discovered by Eckart Schmidt in 2014 and described in [34], QFG #784, #786, #861, #864.
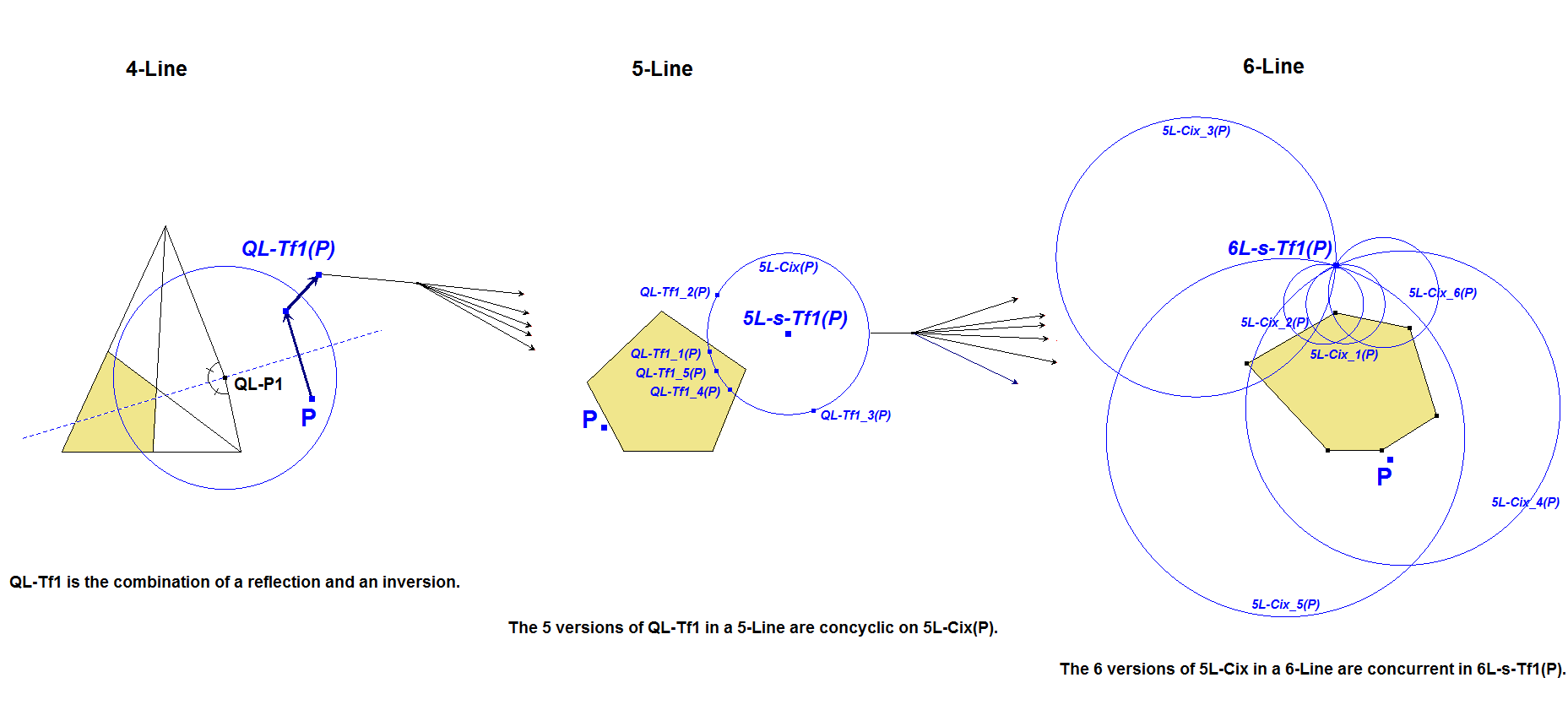
The QL-Tf1-images of a point P wrt the 4-lines of a 5-line lie on a circle, these circles for the 5-lines of a 6-line have a common point 6L-s-Tf1(P).
In steps:
- The 4L-Transformation QL-Tf1 transforms a point P into another point QL-Tf1(P).
- In a 5-Line we have 5 4-Lines and consequently a point P can be transformed into 5 other points which are concyclic on a circle 5L-Cix with center 5L-s-Tf1(P).
- In a 6-Line we have 6 5-Lines and the 6 circles 5L-Cix are concurrent in 6L-s-Tf1(P).
In [34], QFG#920, Eckart Schmidt gave this analyses for Morley’s notes on a similar transformation in a 2n-Lines with an inscribed conic in relationship with the transformations QL-Tf1 (also named CSC), 5L-s-Tf1 (also named 5L-CSC) and 6L-s-Tf1 (also named (6L-CSC):
In §6 of his paper Ref-48 “On the metric geometry of the plane n-line” Morley researched 2n-lines with an inscribed conic. Here are cited his results:“This involution has the following properties:(i) Its center is the Clifford point of the 2p-lines.(ii) The foci are a pair of the involution.(iii) The Clifford point of 2q lines and that of the remaining 2(p-q) lines are a pair of the involution. The Clifford point of two lines means merely their intersection.(iv) The Clifford circle of 2q-1 lines and that of the remaining lines are partners. The Clifford circle of a line is merely the line itself.”For a 4-line, which has always an inscribed conic, this involution is the CSC-transformation.For 6-lines with an inscribed conic this involution is the transformation 6L-CSC, mentioned in QFG #784, #861, #864.Remember: The CSC-images of a point X wrt the 4-lines of a 5-line lie on a circle, these circles for the 5-lines of a 6-line have a common point, the 6L-CSC-image of the point X.For an arbitrary 6L the transformation 6L-CSC holds Morley’s properties (ii) and (iii):wrt (ii): 6L-CSC swaps the foci of the inscribed conics of 5 of 6 lines.wrt (iii): 6L-CSC swaps the intersection of 2 of 6 lines and the Miquel point of the remaining 4 of 6 lines.
But I don’t see any generalization for 2n-CSC!
Properties
- 6L-s-Tf1(P) = 6L-e-P2 for all P on the line at infinity (Cabri-observation).
- 6L-s-Tf1 swaps the foci of the inscribed conics of 5 of 6 lines. See [34], QFG#920.
- 6L-s-Tf1 swaps the intersection of 2 of 6 lines and the Miquel point of the remaining 4 of 6 lines. See [34], QFG#786 and #920.
Estimated human page views: 307
