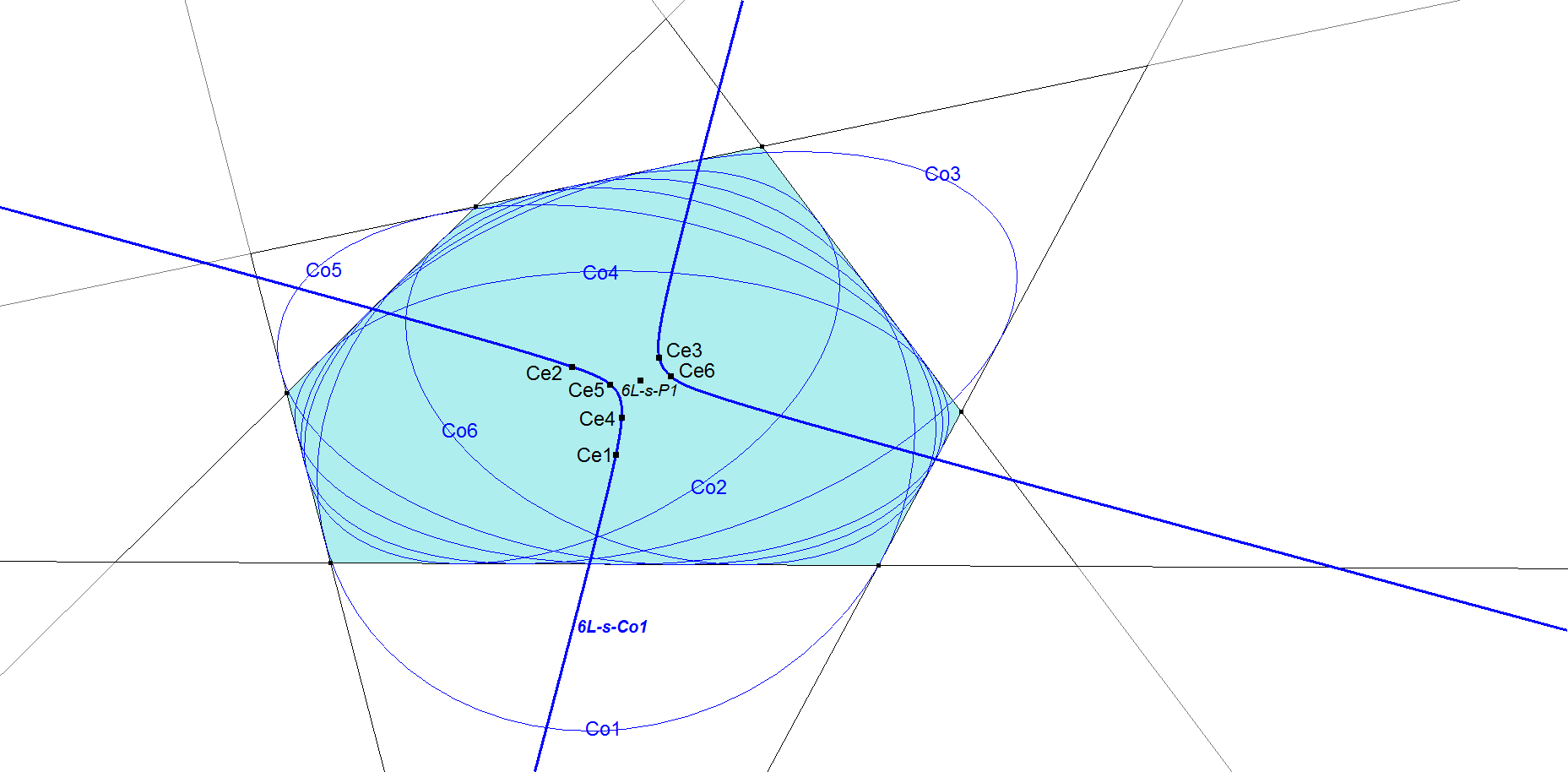
6L-s-Co1: 6L-Conical Center Conic
In a 6-Line we have 6 Component 5-Lines.
When constructing 6 times the Inscribed Conic Centers (5L-s-P1) of the Component 5-Lines they are coconic on 6L-s-Co1.
This feature cannot be extrapolated to a 7-Line.
Relationship with Pascal’s Theorem
Note that for 6L-s-Co1 we have a case of 6 points on a conic without order.
Pascal’s theorem (see Ref-13) is valid for 6 points on a conic with order, stating that if six random points are chosen on a conic and joined by line segments to form a hexagon (6-Gon), then the three pairs of opposite sides of the hexagon meet in three points which lie on a straight line, called the Pascal line of the hexagon. Since Pascal’s theorem is valid for 6 points in a certain order (by stating it is a hexagon (6-Gon)) there are 60 Pascal lines (from the 60 possible 6-Gons) crossing at 20 Points (so-called Steiner Points). These derived 60 lines and 20 points also can be considered as central EPG-objects in 6-Line.
Properties
- In a 7-Line the 7 versions of 6L-s-Co1 concur in 3 points 7L-s-3P1a/b/c.
Estimated human page views: 356
