5L-s-Tf1: the 5L-Schmidt Transformation is a sequel to QL-Tf1: the Clawson-Schmidt Conjugate (often abbreviated with CSC).
Consider an arbitrary point X and its Clawson-Schmidt Conjugates wrt the 5 Component Quadrilaterals of the 5-Line. These points are concyclic on a circle Ci with center X', which shall be the 5L-Tf1-image of X.
This transformation was introduced by Eckart Schmidt. See Ref-34, QFG#713.
Unlike QL-Tf1 (Clawson-Schmidt Conjugate) 5L-s-Tf1 is not a reciprocal transformation, meaning that the output not will be re-transferred into the input by the transformation.
Special is that the Ci-circle of an intersection of two 5L-lines is the circumcircle of the triangle of the remaining three 5L-lines.
The transformation is of the 2nd degree. Therefore it maps lines into conics,
Consider an arbitrary point X and its Clawson-Schmidt Conjugates wrt the 5 Component Quadrilaterals of the 5-Line. These points are concyclic on a circle Ci with center X', which shall be the 5L-Tf1-image of X.
This transformation was introduced by Eckart Schmidt. See Ref-34, QFG#713.
Unlike QL-Tf1 (Clawson-Schmidt Conjugate) 5L-s-Tf1 is not a reciprocal transformation, meaning that the output not will be re-transferred into the input by the transformation.
Special is that the Ci-circle of an intersection of two 5L-lines is the circumcircle of the triangle of the remaining three 5L-lines.
The transformation is of the 2nd degree. Therefore it maps lines into conics,
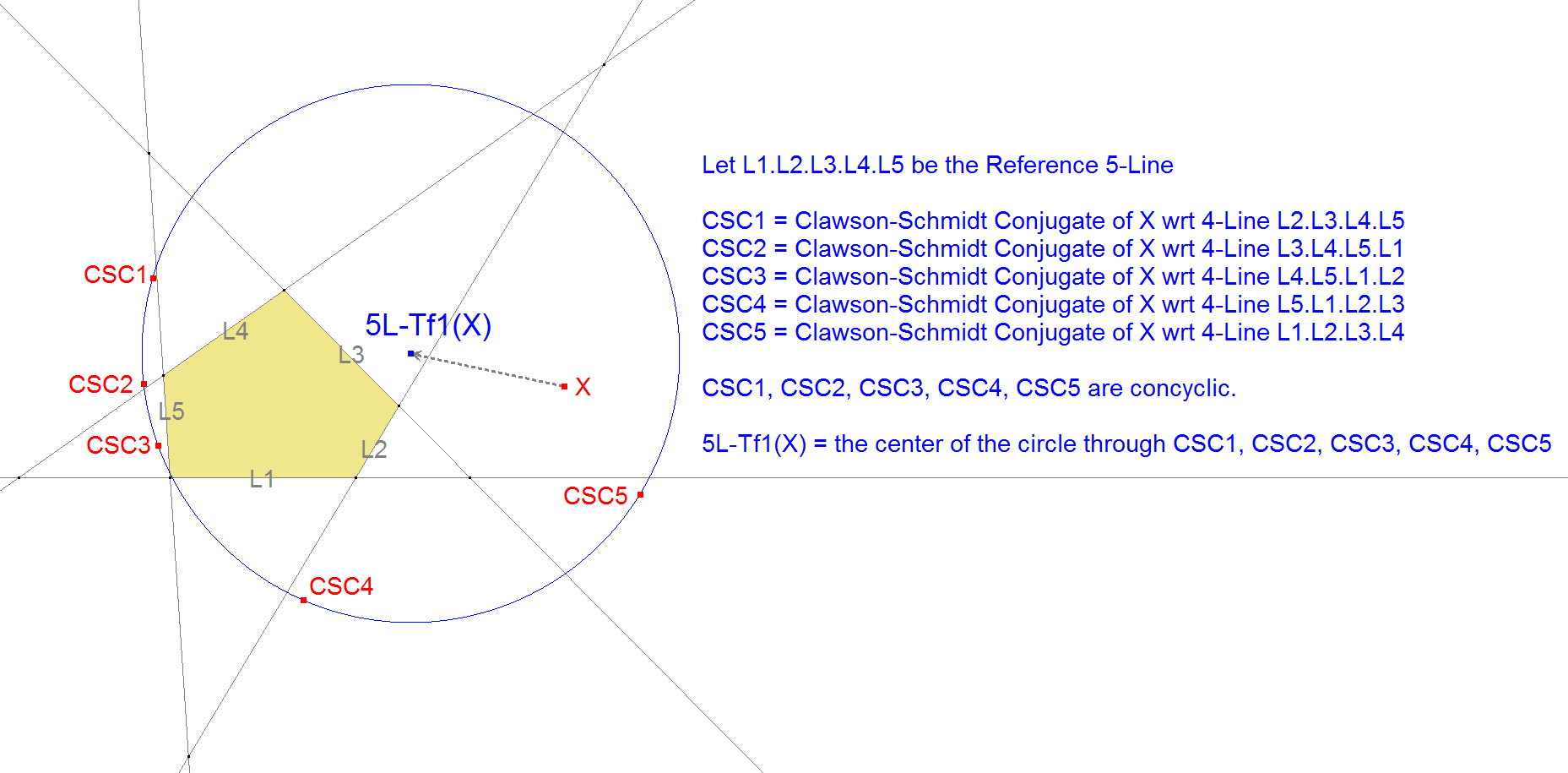
Properties:
• the 5L-s-Tf1-image of 5L-o-P2.5L-n-P3 is a conic, centered in 5L-s-P1, containing 5L-o-P2 (Eckart Schmidt, QFG#713).
• the 5L-s-Tf1-image of any line contains 5L-o-P2 (Eckart Schmidt, QFG#713).
• 5L-s-Tf1 swaps the foci of the inscribed conic (Eckart Schmidt, QFG#722).
• the image of 5L-o-P2 is the reflection in 5L-s-P1 (Eckart Schmidt, QFG#722).
• the image of the QL-P1-circle is the line at infinity (Eckart Schmidt, QFG#722).
• the image of a QL-P1-point is the point at infinity of a perpendicular line to the corresponding QL-line (Eckart Schmidt, QFG#722).
• the image of the QL-P4-circle is a hyperbola (Eckart Schmidt, QFG#722).
• the image of the main axis of the inscribed conic is a conic through the foci and 5L-p1, symmetric to the second axis (Eckart Schmidt, QFG#722).
• The CSC-circle of an intersection of 2 5L-lines is the circumcircle of the triangle of the remaining 3 5L-lines (Eckart Schmidt, QFG#754).
• The 5L-s-Tf1-image of the QL-P1-circle is the line at infinity (Eckart Schmidt, QFG#754).
• The CSC-circles of points on the QL-P1-circle degenerate to lines, tangent to the inscribed conic of the 5L (Eckart Schmidt, QFG#754).
• For the QL-P1-points the degenerated CSC-circles are the lines Li of the 5L (Eckart Schmidt, QFG#754).
• For intersections of a line Li and the QL-P1-circle the degenerated CSC-circle contains the 2nd intersection and QL-P1 of the remaining QL (Eckart Schmidt, QFG#754).
• For a point X on the QL-P1-circle the degenerated CSC-circle cuts the QL-P1-circle in 2 points, whose connections with X are tangent to the inscribed conic (Eckart Schmidt, QFG#754).
• For 2 diametral points on the QL-P1-circle the degenerated CSC-circles intersect on a line perpendicular 5L-o-P2.5L-s-P1 (Eckart Schmidt, QFG#754).
• The CSC-circle of 5L-s-P2 contains 5L-s-P3 and the CSC-circle of 5L-s-P3 contains 5L-s-P2 (Eckart Schmidt, QFG#754).
• For 2 points inverse wrt the QL-P1-circle the 5L-s-Tf1-images are symmetric wrt 5L-s-P1 (Eckart Schmidt, QFG#754).
• 5L-s-Tf1(Li^Lj) = Circumcenter (Lk,Ll,Lm), where (i,j,k,l,m) are different numbers from (1,2,3,4,5) (Bernard Keizer, QFG#786).
For those interested in more properties follows here QFG#762 from Eckart Schmidt:
wrt 5L-s-Tf1 (see #713, #722, #754, #769) further properties:
Remember: 5L-s-Tf1 maps a point X to the center of the concyclic 5 CSC-images of X.
... Let F1 and F2 be the foci of the inscribed conic of 5L, swapped by 5L-s-Tf1 (see #722).
... Let F1° and F2° be their inverses wrt the QL-P1-circle, then 5L-s-Tf1(Fi°) = Fi.
... So there are two points F1 and F2° with 5L-s-Tf1-image F2 ...
... Let X be the intersection of F1.F2° and F1°.F2, then holds 5L-s-Tf1(X) = 5L-o-P2.
... Lines through X have a line through 5L-o-P2 as 5L-s-Tf1-image...
... with intersections on an orthogonal hyperbola Hy ...
... through X, 5L-o-P2, F1° and F2° and a tangent in 5L-o-P2 through 5L-s-P1.
... (The inverse of Hy wrt the QL-P1-circle is the strophoid of 5L-o-P2.5L-s-P1 with pole 5L-o-P2 and fixed point Y, which is the inverse wrt the QL-P1-circle of the reflection of 5L-o-P2 in the center of Hy.)
... The transformation 5L-s-Tf1 has three fixed points. They are the intersections of the orthogonal hyperbola Hy and its 5L-s-Tf1-image (a curve of degree 5).
... Generally there are two preimages P' and P'' of a point P wrt 5L-s-Tf1.
... The line P'P'' contains the point X (see above).
... The CSC-circles of P' and P'' are inverse wrt a circle Ci(P) round P with radius sqr(PF1*PF2).
... Construction of the second Point P'', if P and P' are known: Let CSC-Ci(P') be the CSC-circle of P', then the inverse wrt Ci(P) is CSC-Ci(P'') and the common point of the CSC-images of CSC-Ci(P'') is P''.
The properties are only CABRI-observations!