5L-s-P3: 5L-X(265)-Hofstadter Point
The X(265)-circles of the 4-Lines (described at QL-P29: Circumcenter QL-X(265)-Quadrangle) in a 5-Line have one point in common (See [34], QFG#82, Seiichi Kirikami).
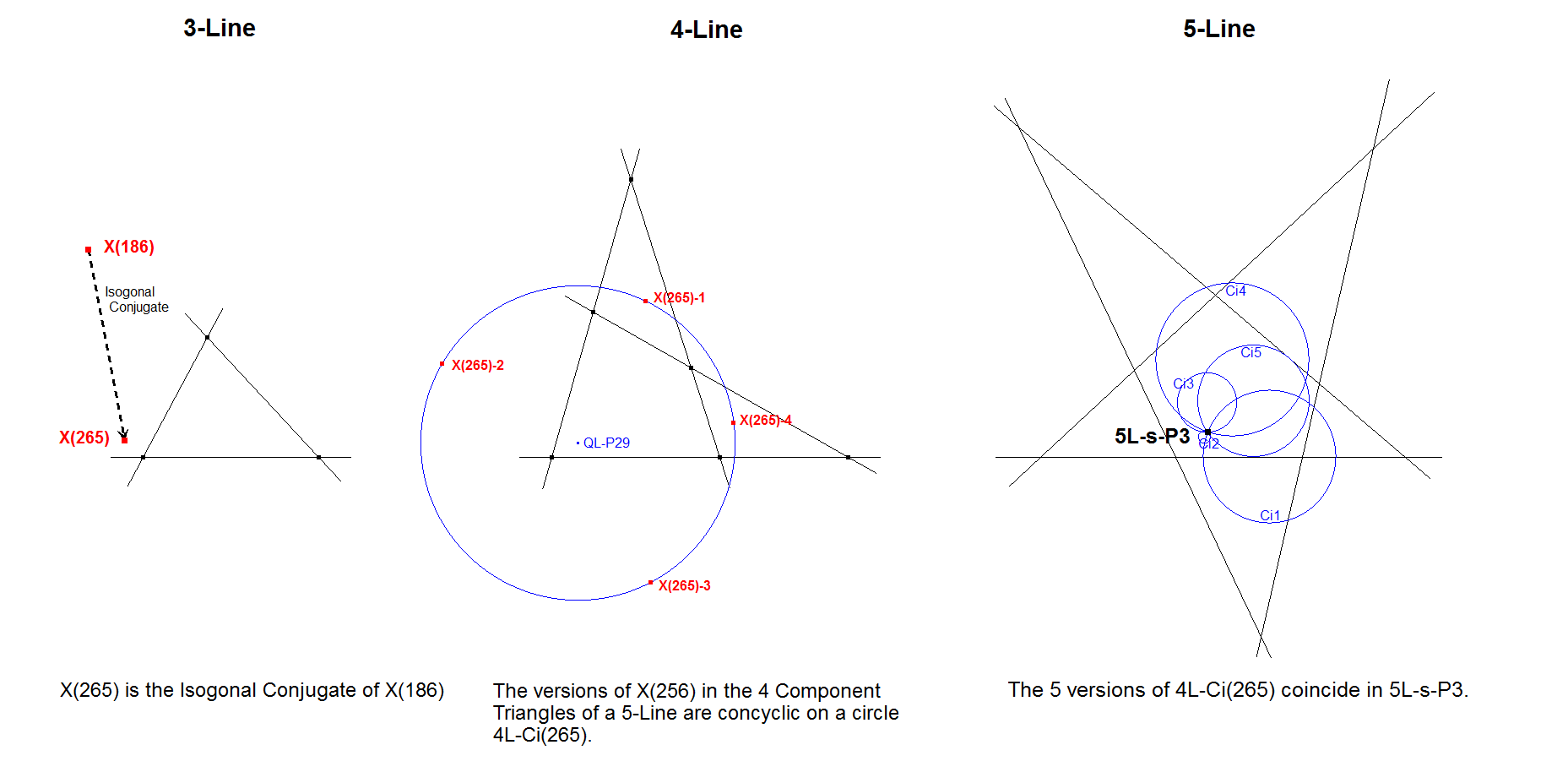
This sequence of Point –> Circle –> Common-point is typical for Hofstadter Triangle Points H(n) for n = integer <> -1, 0, +1.
For explanation of Hofstadter Triangle Points see remarks 5L-s-P2.
Properties
- The same procedure exists for X(3), which also is a Hofstadter Point in a 3-Line. In a 4-Line the X(3)-versions are concyclic on 4L-n-Ci1 and the 5 versions of this circle in a 5-Line concur in 5L-n-P1. However this sequel continues infinitely for n>5, which is not the case for X(265).
- 5L-s-P3 lies on the circle determined by the 5 QL-Tf1 images (wrt the component QL’s) of 5L-s-P2. See [34], Eckart Schmidt, QFG-message#2707.
Estimated human page views: 313
