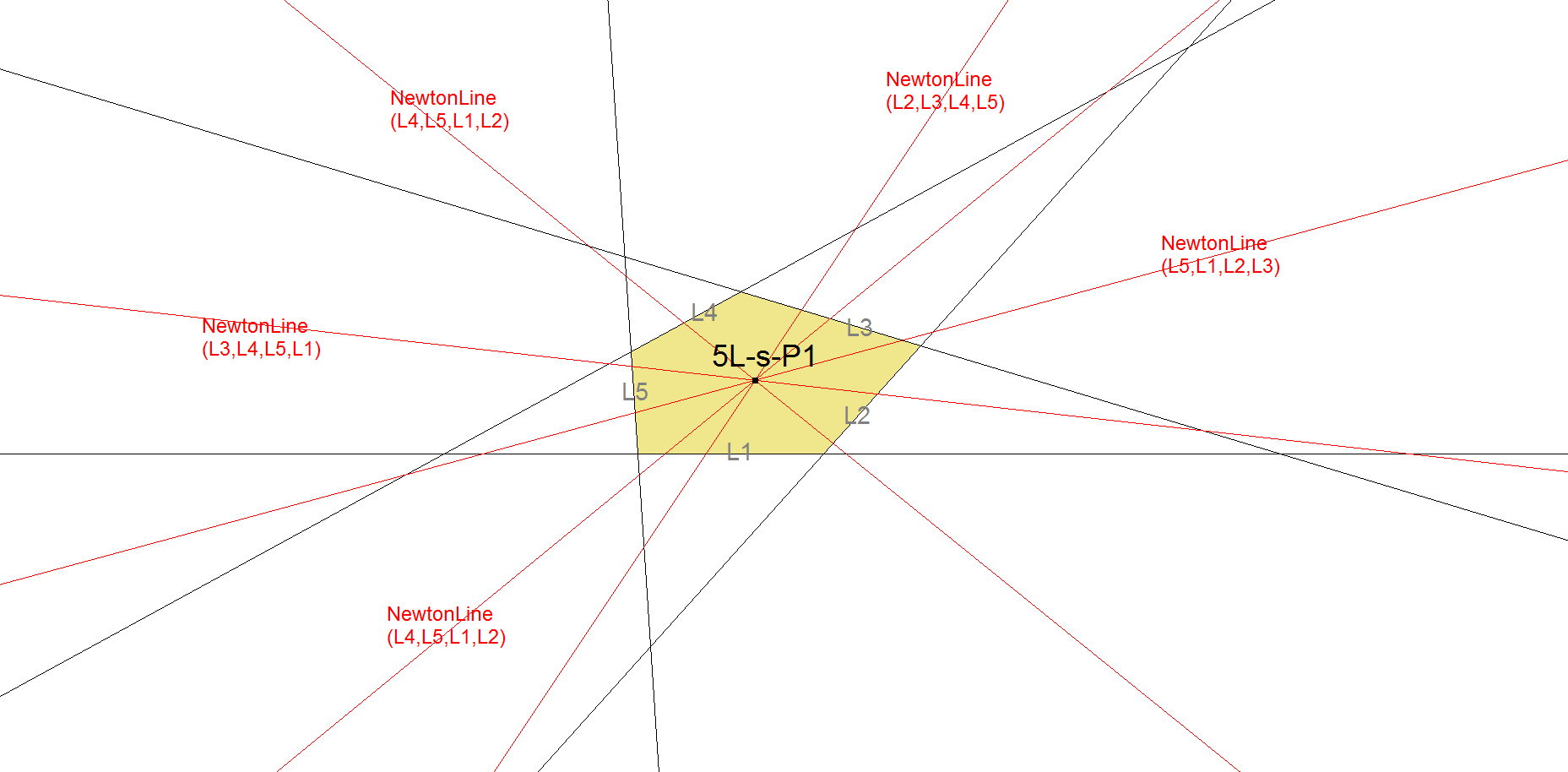
5L-s-P1: 5L-Inscribed Conic Center
It is well known that in a system of 5 random lines a unique inscribed conic can be constructed. This conic is 5L-s-Co1 and 5L-s-P1 is the center of this conic.
In a 4-Line the Newton Line (QL-L1) is the locus of the centers of all 4L-inscribed conics. Consequently the Newton Lines of the 5 Component 4-Lines pass through the Center of the 5L-Inscribed Conic.
Construction
A simple way of construction of 5L-s-P1 is by drawing the Newton Lines (QL-L1) of two Component 4-Lines. The intersection point of these lines will be the center of the 5L-Inscribed Conic.
Coordinates
When using barycentric coordinates/coefficients:
L1=(1:0:0), L2=(0:1:0), L3=(0:0:1), L4=(l:m:n), L5=(L:M:N)
then 5L-s-P1 has coordinates:
( m n L (M – N) – M N l (m – n) :
n l M (N – L) – N L m (n – l) :
l m N (L – M) – L M n ( l – m) )
Properties
- 5L-s-P1 is collinear with 5G-s-P1, 5G-s-P2, 5G-s-P5 for every 5G-version of the 5L.
- 5L-s-P1 is the 4th harmonic point of 5G-s-P1 wrt 5G-s-P2 and 5G-s-P5 for every 5G-version of the 5L. See [66], QPG-message #1152.
Estimated human page views: 316
