The Regular PDN-n-Gons are derived from irregular random n-Gons following the rules of the Petr-Douglas-Neumann Theorem. The Petr-Douglas-Neumann Theorem asserts the following.
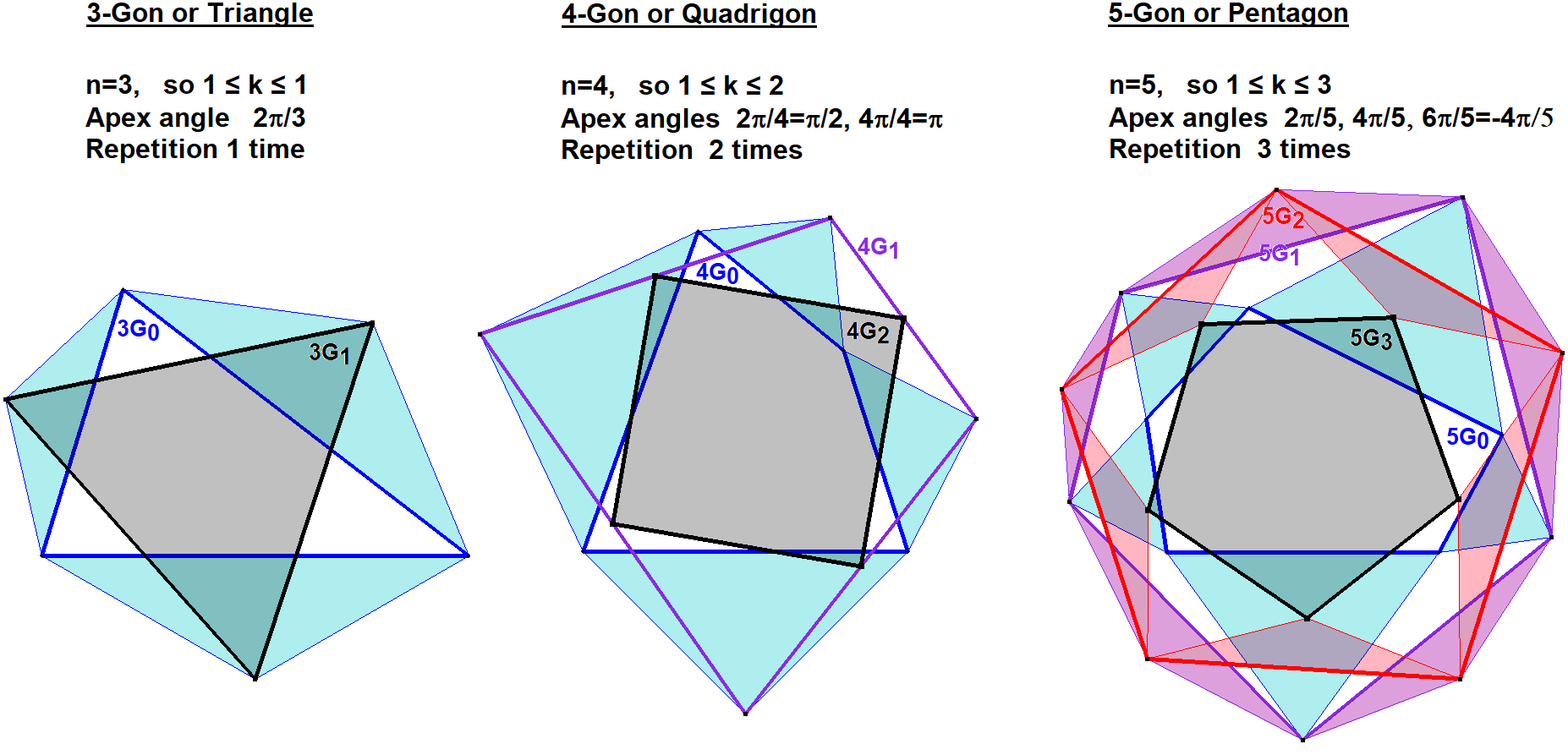
If isosceles triangles with apex angles 2kπ/n are erected on the sides of an arbitrary n-Gon nG0, and if this process is repeated with the n-Gon formed by the free apices of the triangles, but with a different value of k, and so on until all values 1 ≤ k ≤ n − 2 have been used (in arbitrary order), then a Regular n-Gon nGn−2 is formed whose centroid coincides with the centroid of nG0.
For extra information see Ref-13 and Ref-35b.
If isosceles triangles with apex angles 2kπ/n are erected on the sides of an arbitrary n-Gon nG0, and if this process is repeated with the n-Gon formed by the free apices of the triangles, but with a different value of k, and so on until all values 1 ≤ k ≤ n − 2 have been used (in arbitrary order), then a Regular n-Gon nGn−2 is formed whose centroid coincides with the centroid of nG0.
For extra information see Ref-13 and Ref-35b.
Stepwise construction
• Draw the random n-Gon nG0. Let’s say a 5-Gon. Therefore n = 5.
• Determine the number of iterations (k) we need in order to construct the final Regular n-Gon. This number is k = n - 2, so in our case we have 3 iterations to go, in order to construct nG1, nG2 and the final regular n-Gon nG3.
• Determine the Apex angles we have to use. They are defined as 2kπ/n (1 ≤ k ≤ n – 2), so in our case we have Apex angles 2π/5, 4π/5 and 6π/5. We can use these Apex angles for constructing nG1, nG2, nG3 in next steps in any order you wish and one at a time. The final result will be a regular n-Gon. Note, when the Apex angle is π, then the Apex will be the midpoint of the sideline it is erected on. For example, when n=4, then we have an Apex angle of π. When π < Apex angle < 2π then diminish the Apex angle with 2π and we will get a negative Apex angle that will be erected at the other side of the sideline at hand.
• Construct nG1 by erecting isosceles triangles at each sideline of nG0, all with the same chosen first Apex angle. These Apexes will be the vertices of nG1.
• Construct nG2 by erecting isosceles triangles at each sideline of nG1, all with the same chosen second Apex angle. These new Apexes will be the vertices of nG2.
• Construct the final regular n-Gon nG3 by erecting isosceles triangles at each sideline of nG2, all with the last not used Apex angle. The new Apexes will be the vertices of nG3.
