5G-s-P2 1st 5G-Kirikami Point
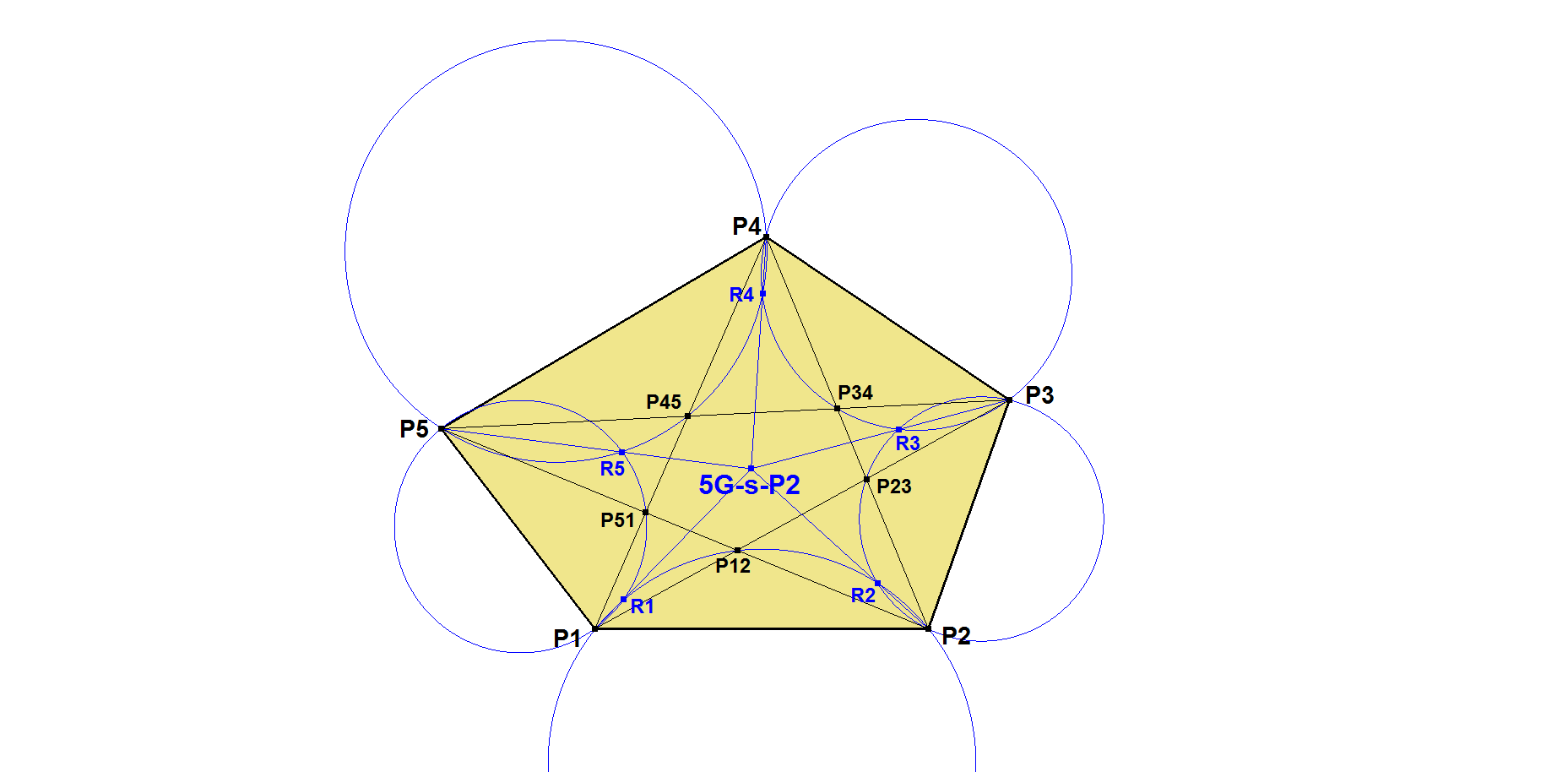
Given a Pentagon P1P2P3P4P5. We denote the intersection of PiPi+2 and Pi-1Pi+1 by Pii+1. We denote the circumcircle of PiPii+1Pi+1 by Cii+1. We denote the second intersection of Ci-1i and Cii+1 by Ri. Then PiRi concur in a point P.
See [34], Seiichi Kirikami, QFG#721.
See [59c], Telv Cohl, same problem with proof.
Coordinates
Let P1,P2,P3,P4,P5 have these barycentric coordinates:
P1=(0:1:0), P2=(0:0:1), P3=(1:0:0), P4=(p:q:r) and P5=(P:Q:R).
Then 5G-s-P2 has coordinates: p (P+Q) : Q (p+q) : – r R).
Calculation Seiichi Kirikami. See [34], QFG#751.
Properties
- 5G-s-P1, 5G-s-P2, 5G-s-P5 and 5L-s-P1 are collinear.
- 5G-s-P2 is the 4th harmonic point of 5G-s-P5 wrt 5G-s-P1 and 5L-s-P1 for every 5G-version of a 5-Line. See [66], QPG-message #1152.
- 5G-s-P2(P1.P2.P3.P4.P5) = 5G-s-P5(P1.P3.P5.P2.P4). See [66], QPG-message #1398.
- 5G-s-P2(P1.P3.P5.P2.P4) = 5G-s-P5(P1.P2.P3.P4.P5)
Estimated human page views: 318
