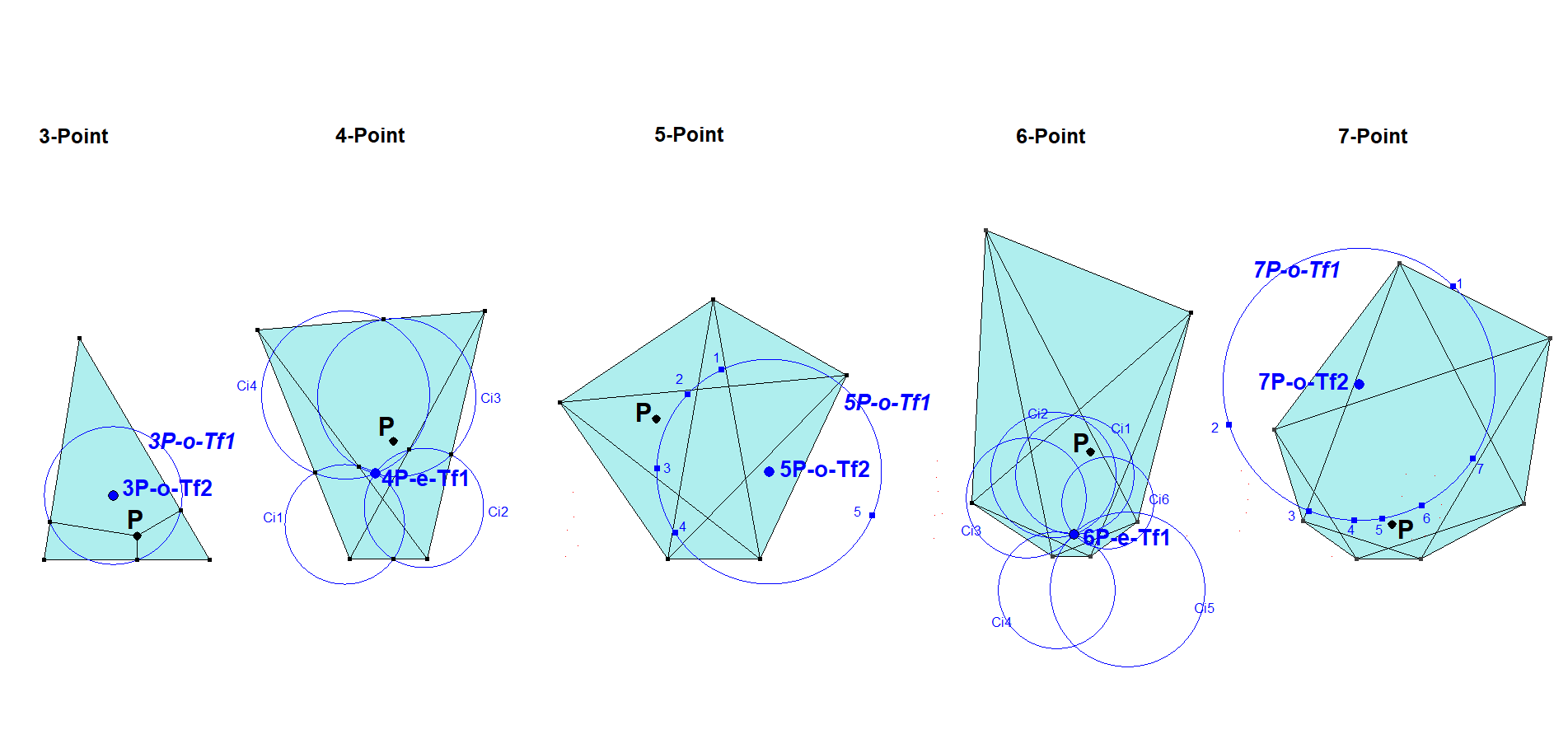
nP-e-Tf1 nP-Pedal Point
nP-o-Tf1 nP-Pedal Circle
nP-o-Tf2 nP-Pedal Circle Center
There is an alternating sequence of circles & circle centers in n-Points, when n=odd and common circle points in n-Points, when n=even.
nP-e-Tf1 is a generic designation, denoting the specific transformations 4P-e-Tf1, 6P-e-Tf1, 8P-e-Tf1, etc.. They are point to point transformations in an n-Point for n=even.
nP-o-Tf1 is a generic designation, denoting the specific transformations 3P-o-Tf1, 5P-o-Tf1, 7P-o-Tf1, etc.. They are point to circle transformations in an n-Point for n=odd.
nP-o-Tf2 is a generic designation, denoting the specific transformations 3P-o-Tf2, 5P-o-Tf2, 7P-o-Tf2, etc.. They are point to point transformations in an n-Point for n=odd.
Definition
The Pedal Triangle of P wrt a reference triangle ABC is the triangle formed by the Pedal Points (projection points) of P on the sidelines of the triangle ABC.
The development of nP-o-Tf1, nP-o-Tf2, nP-e-Tf1 for increasing n is best understood by starting with n=3.
- 3-Point: The 3 Pedal Points of P wrt a 3-Point define a Circle 3P-o-Tf1 with center 3P-o-Tf2.
- 4-Point: The 4 circles 3P-o-Tf1 of the component triangles intersect at a common point 4P-e-Tf1.
- 5-Point: The 5 common points 4P-e-Tf1 of the component 4-Points lie on a circle 5P-o-Tf1 with center 5P-o-Tf2.
- 6-Point: The 6 circles 5P-o-Tf1 of the component 5-Points intersect at a common point 6P-e-Tf1.
- 7-Point: The 7 common points 6P-e-Tf1 of the component 6-Points lie on a circle 7P-o-Tf1 with center 7P-o-Tf2.
- etc.
It was discovered by Ngo Quang Duong in [34], QFG#2759.
His proof is as follows:
- For 4 points, we consider the inversion with center P, power k (I(P,k)). Pij is the orthogonal projection of P on PiPj. I(P,k)(Pi)=P’i. Since P12, P13, P14, P are concyclic(they lie on the circle of which diameter is PP1) then P’12, P’13, P’14 are collinear. Similarly, P’21, P’23, P’24 are collinear,… Hence after the inversion, it reduces to Miquel’s theorem (Clifford’s theorem for n=4).
- For 5 points, we consider the same inversion. Since P, P12, P13, P14, P15 are concyclic then P’12, P’13, P’14, P’15 are collinear. Now, it reduces to Clifford’s theorem for n=5.
- etc…
And about the antipedal circles, we can apply the Clifford’s theorem directly.
Correspondence with ETC/EQF
In a 3-Point-configuration:
In a 4-Point-configuration:
Properties
- When n = 5 and P lies on the 5P-Circumscribed Conic, then the 5P-Pedal Circle 5P-o-Tf1(P) diminishes to a point and its center 5P-o-Tf2(P) will coincide with 5P-s-Tf3(P) = CO-Tf3-1(P).
- The 4 versions of the 3P-o-Tf1(Pi)-Circles (3P-o-Tf1(Pi) applied to triangles PjPkPl) coincide in a common point which is QA-P2 of the Reference Quadrangle QA0. The 4 versions of 3P-o-Tf2(Pi)-Circlecenters (3P-o-Tf2(Pi) applied to triangles PjPkPl) form a Quadrangle QA1 which is similar to the Reference Quadrangle QA0. QA-P2 of QA0 coincides with QA-P4 of QA1.
Estimated human page views: 633
