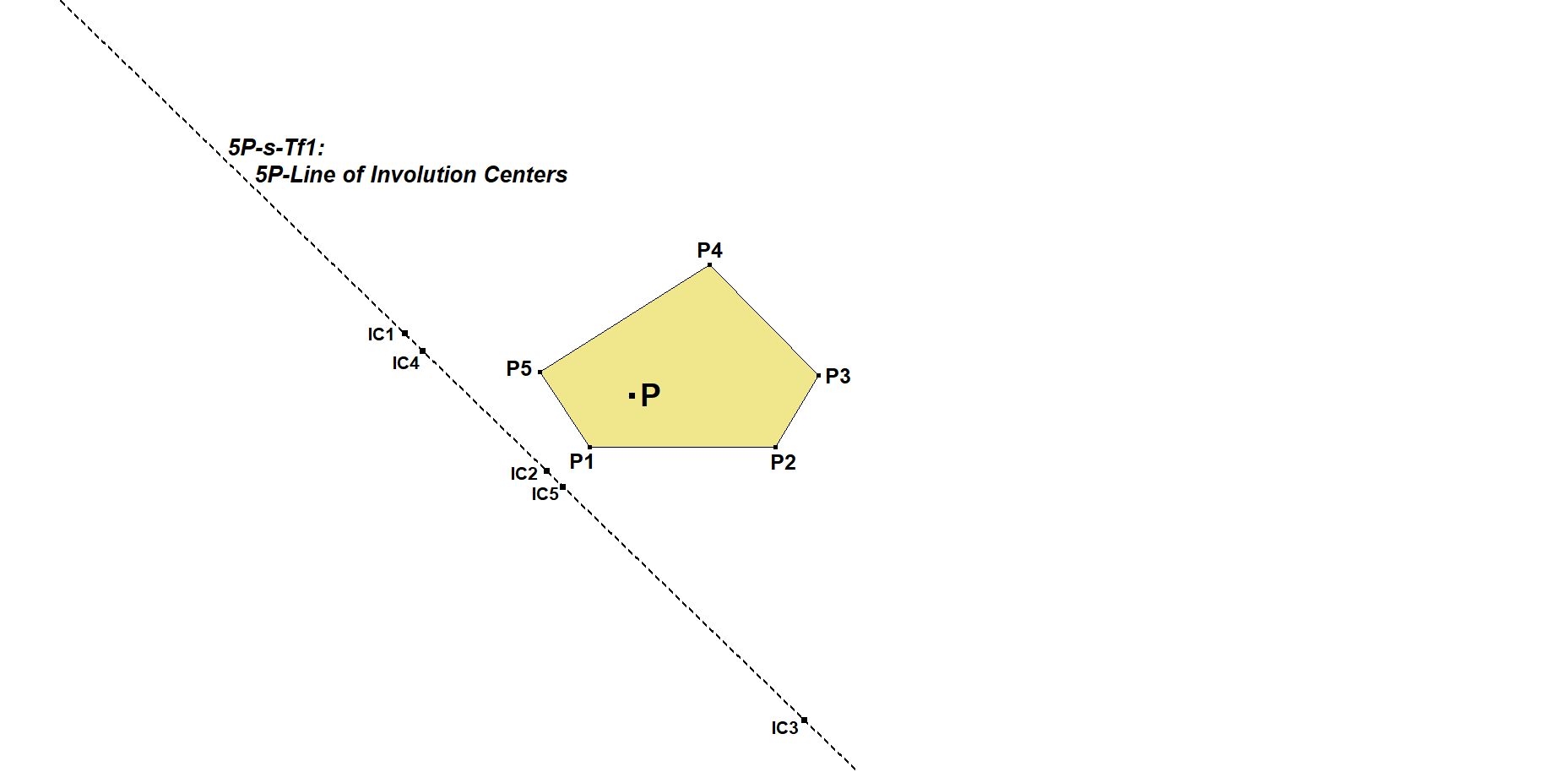
5P-s-Tf1: 5P-Line of Involution Centers
5P-s-Tf1 is a transformation that maps some point P into a line of Involution Centers.
Each 5-Point (Pentangle) contains 5 4-Points (Quadrangles).
In a Quadrangle QA-Tf1(P) is the Involution Center of the tangent line at P to the conic through the vertices of the reference quadrangle and P.
The 5 versions of QA-Tf1(P) are collinear on 5P-s-Tf1(P).
Properties
- When P = 5P-s-P1, then 5P-s-Tf1(P) = Line at Infinity.
- When P lies on the 5P-circumscribed conic 5P-s-Co1, then 5P-s-Tf1(P) is the tangent at P to 5P-s-Co1.
- 5P-s-Tf1(P) // 5P-s-Tf2(P).
- d(P,5P-s-Tf1(P)) = d(5P-s-Tf1(P),5P-s-Tf2(P)) = d(P,5P-s-Tf2(P)) / 2.
- P is the Railway Watcher of lines 5P-s-Tf1(P) and 5P-s-Tf1(P). See QL-L-1.
- 5P-s-Tf1 of points P on a line L give a parabola, tangent to 5P-s-Co1 in the intersection points with L. Its axis is parallel to the line through 5P-s-P1 and the pole of L wrt 5P-s-Co1. See [34], Eckart Schmidt, QFG#2792.
- Parallels to 5P-s-Tf1,2(P) through P for points P on a line L give a parabola. For more information on this parabola see [34], Eckart Schmidt, QFG#2792.
Estimated human page views: 307
