nL-o-P2: nL-Clifford's Circle Center

---

There is an alternating construction of circles/circle centers (odd case) and common circle points (even case) in the sequence of n-Lines with increasing n.
Morley described this sequence as Clifford’s Chain in Ref-48, page 103 and Ref-37.
It is best to understand with numbers:
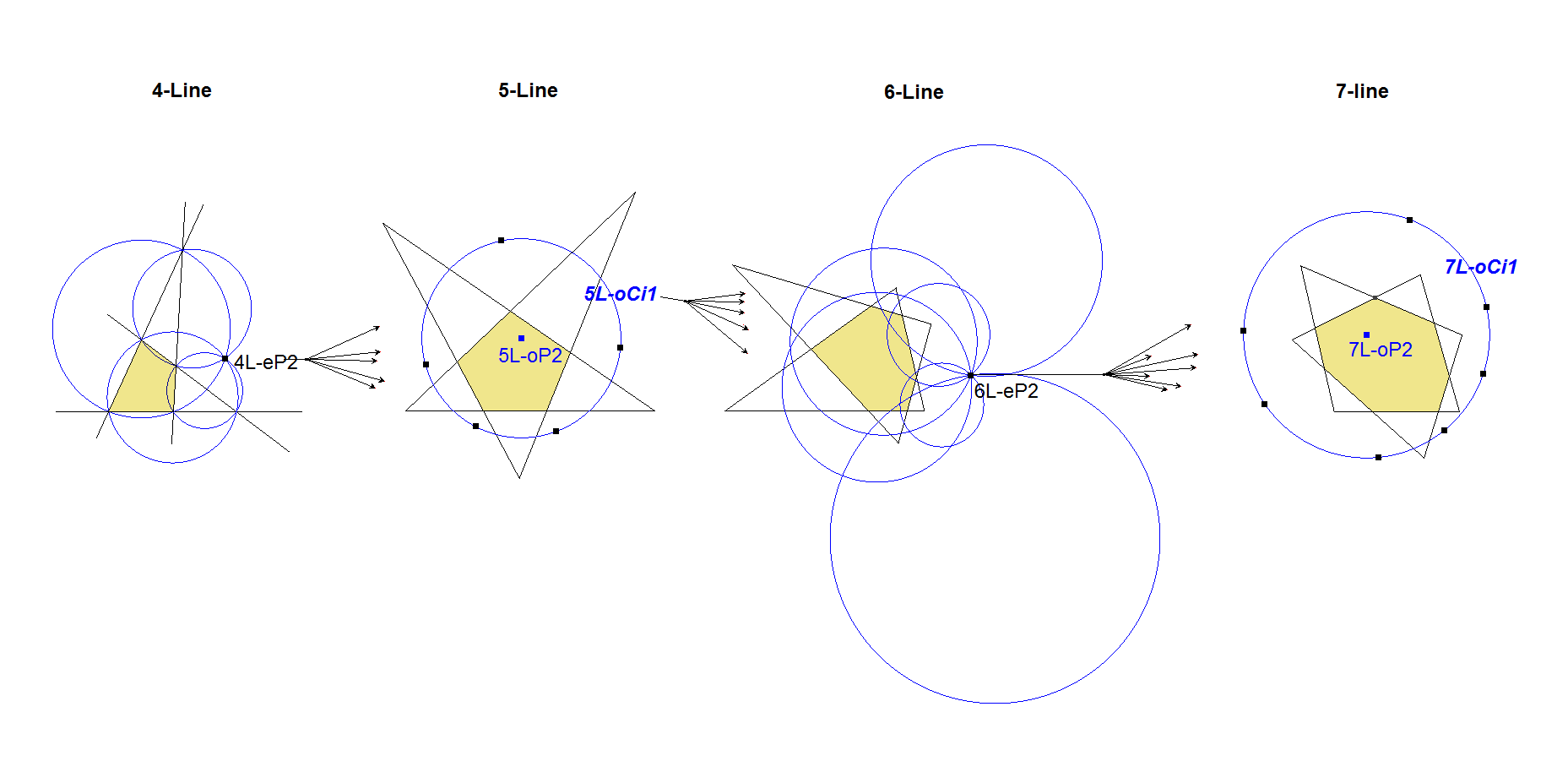
• 4 Clifford’s Circles of a 4-Line (Circumscribed circles of the component triangles) intersect at a common point 4L-e-P2: Clifford’s Point, which is QL-P1 (Miquel Point) in the case of a 4-Line.
• 5 Clifford’s Points of a 5-Line (Miquel Points of the 5 component 4-Lines) lie on a circle 5L-o-Ci1: Clifford’s Circle with center 5L-o-P2: 5L-Clifford’s Circle Center.
• 6 Clifford’s Circles of a 6-Line (5L-o-Ci1 of the 6 component 5-Lines) intersect at a common point 6L-e-P2: 6L-Clifford’s Point.
• 7 Clifford’s Points of a 7-Line (6L-e-P2 of the 7 component 6-Lines) lie on a circle 7L-o-Ci1: 7L-Clifford’s Circle with center 7L-o-P2: 7L-Clifford’s Circle Center.
• 8 Clifford’s Circles of a 8-Line (7L-o-Ci1 of the 8 component 7-Lines) intersect at a common point 8L-e-P2: 8L-Clifford’s Point.
• 9 Clifford’s Points of a 9-Line (8L-e-P2 of the 9 component 8-Lines) lie on a circle 9L-o-Ci1: 9L-Clifford’s Circle with center 9L-o-P2: 9L-Clifford’s Circle Center.
• etc.

Correspondence with ETC/EQF:
When n=3, then nL-o-P2 = X(3) and nL-o-Ci1 = Triangle circumcircle.
When n=4, then nL-e-P2 = QL-P1.

Properties:
• In a 5-Line 5L-o-Ci1 = Miquels Pentagon Circle and 5L-o-P2 = Center of Miquels Pentagon Circle.
   See Ref-13, Miquel's Pentagram Theorem. See Ref-34, QFG#1999.

---