nL-n-P8: nL-MVP Centroid
nL-n-P8 is the nL-Mean Vector Point (see nL-n-Luc4) of X(2), the Triangle Centroid.
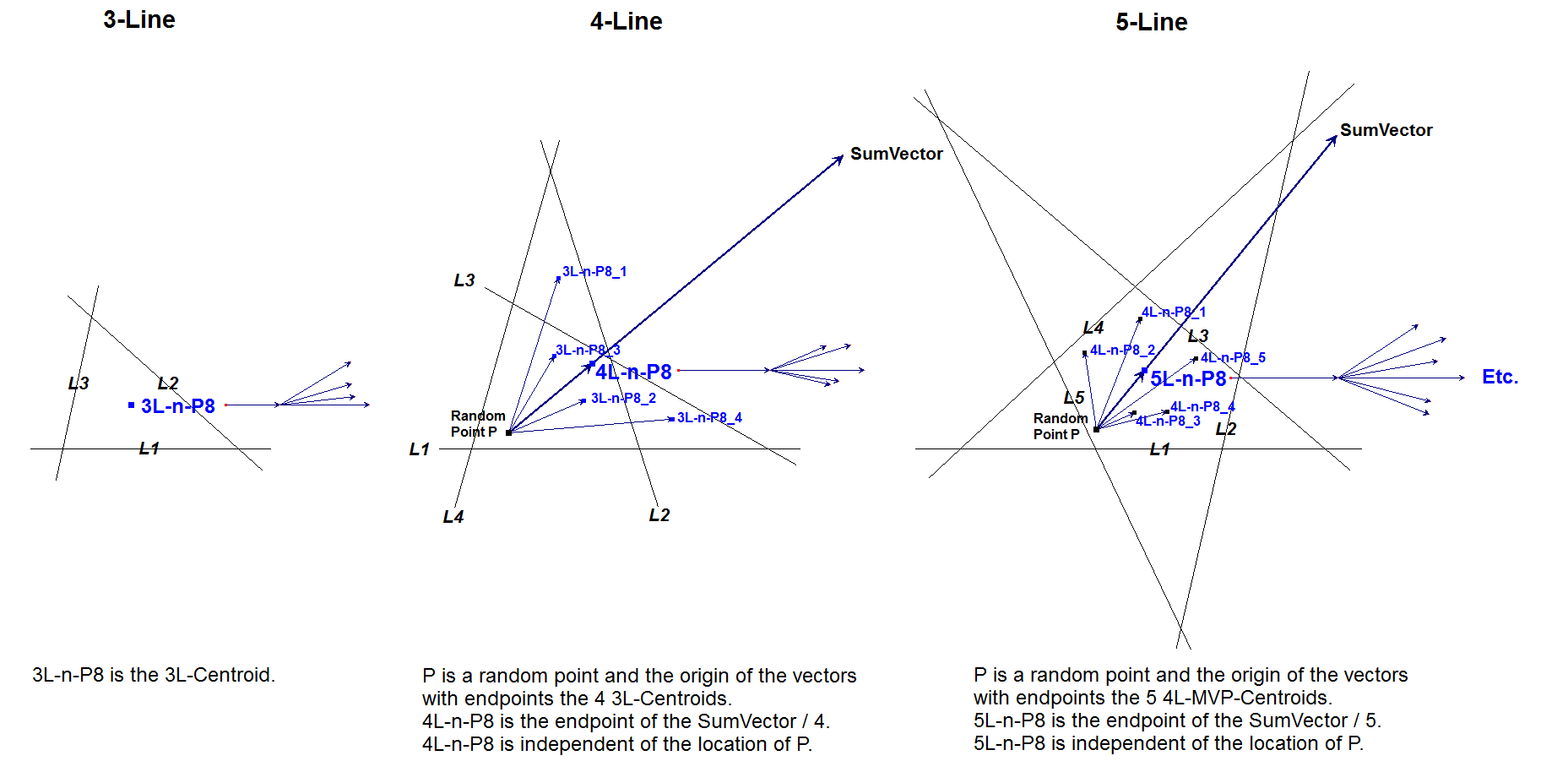
Another construction of nL-MVP Centroid
The 4L-MVP-Centroid QL-P12 is constructed from 3L-MVP-Centroid X(2) using 4-polar Centroids.
The 5L-MVP-Centroid can be generated from 4L-MVP-Centroid QL-P12 in a similar way using 5-polar centroids.
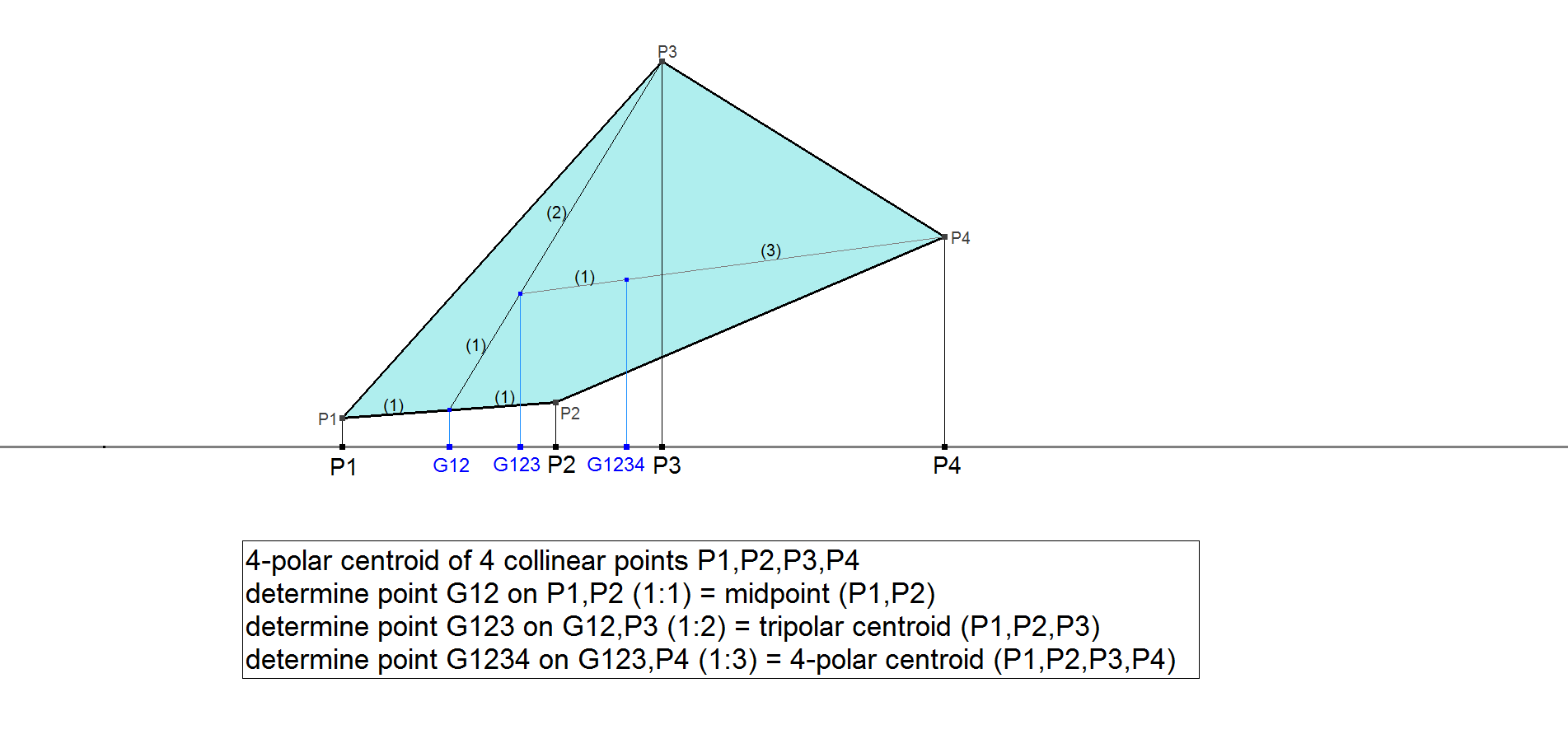
Each line of the 5 lines in a 5-Line has 4 intersection points with the 4 other lines.
These 4 collinear points can be seen as a “flat” quadrangle and have a corresponding Quadrangle Centroid also called here a 4-polar Centroid.
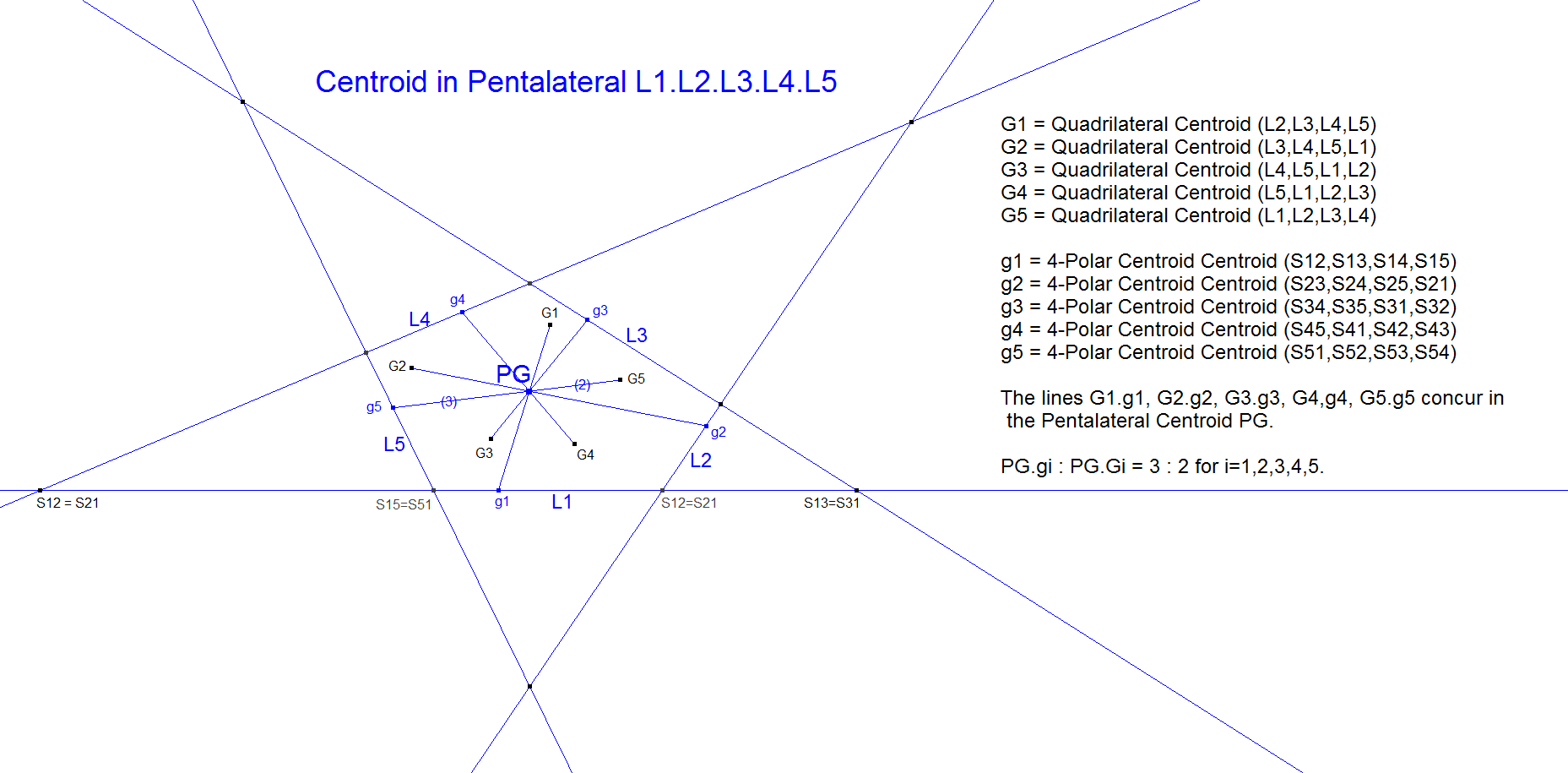
In a 5-Line there are 5 Component Quadrilaterals. The lines connecting the QL-Centroids of these Component Quadrilaterals with their corresponding 4-polar centroids concur in one point being 5L-n-P8.
In the same way the 6L-MVP-Centroid also can be generated from the 5L-MVP-Centroid, etc.
Correspondence with ETC/EQF
- In a 3-Line:
- In a 4-Line we find:
Properties
- nL-n-P8, nL-n-P9, nL-n-P10 and nL-n-P11 are collinear. Their mutual distance ratios correspond with the mutual distance ratios from triangle centers X(2), X(3), X(4) and X(5).
- nL-n-P8 is also the Homothetic Center of the Reference n-Line and the n-Line formed by the lines through the n (n-1)L-versions of nL-n-P8 parallel to the omitted Line. So starting with X(2) in a triangle it can be gradually constructed up to all higher n-levels in this way.
Estimated human page views: 328
