nL-n-Ci2: nL-Second Circle
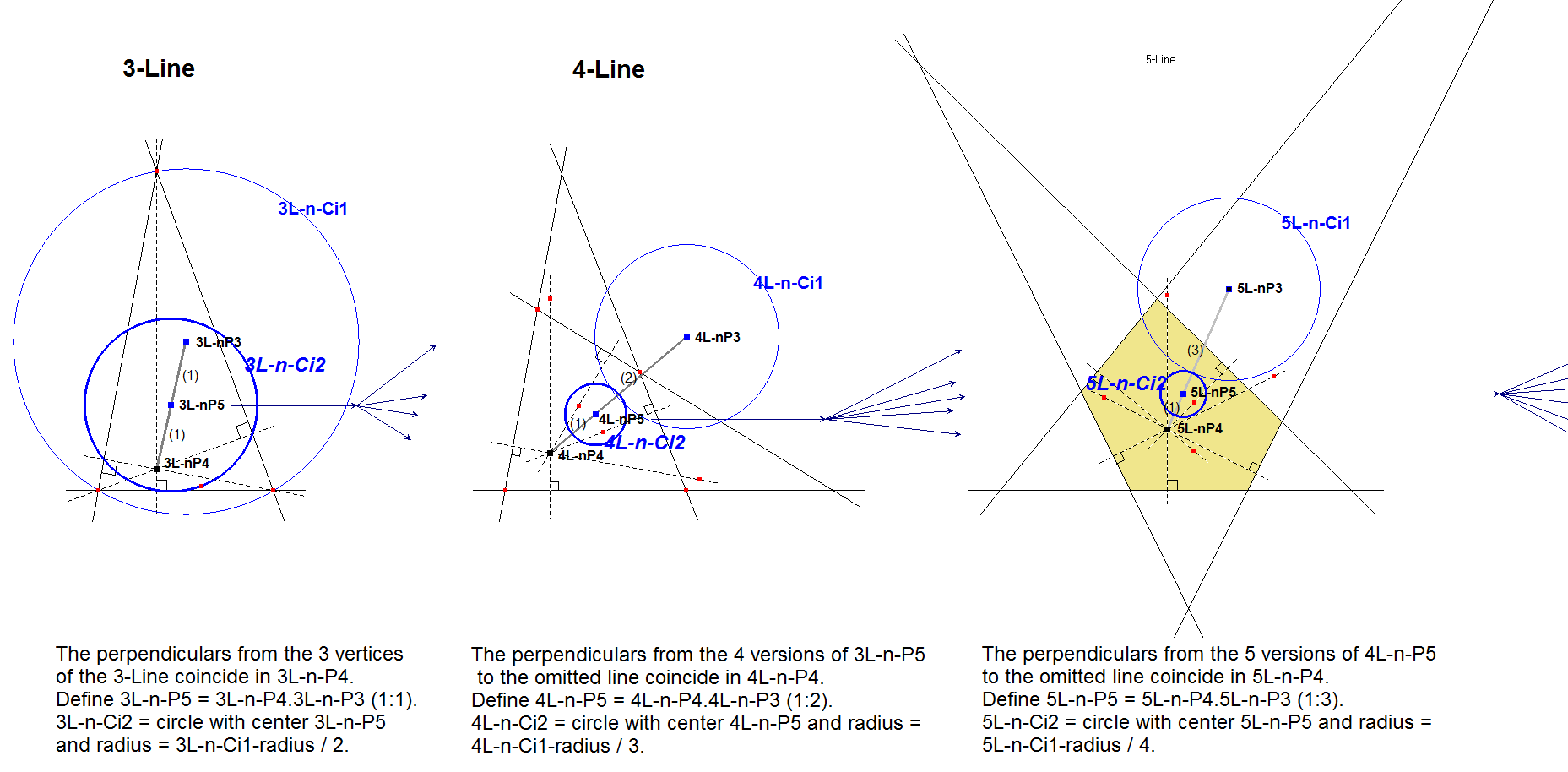
Morley defines a 2nd circle with radius 1/(n-1) radius of the center circle (1/2 for the triangle and 1/3 for the quadrilateral, etc.). The center of this circle is nL-n-P5.
nL-n-Ci2 can be used for the construction of nL-n-P4.
Construction of nL-Ci2
nL-n-Ci2 can be constructed in a recursive way (first in a 3-Line, then in a 4-Line, .. up to an n-Line):
- Construct the perpendiculars of the n versions of (n-1)L-n-P5 of the Component (n-1)-Lines to the omitted line. They will concur in nL-n-P4.
- Construct nL-n-P5 = nL-n-P4.nL-n-P3 (1 : n-1).
- Construct circle nL-n-Ci2 with center nL-n-P5 and radius 1/(n-1) times the radius of nL-Ci1.
Correspondence with ETC/EQF
- When n=3, then nL-n-Ci2 = Euler Circle (or Nine-point Circle or Feuerbach Circle) in a Triangle.
- When n=4, then nL-n-Ci2 = Circle centered in QL-P30 with radius = 1/3 of the radius of QL-Ci3.
Properties
Estimated human page views: 327
