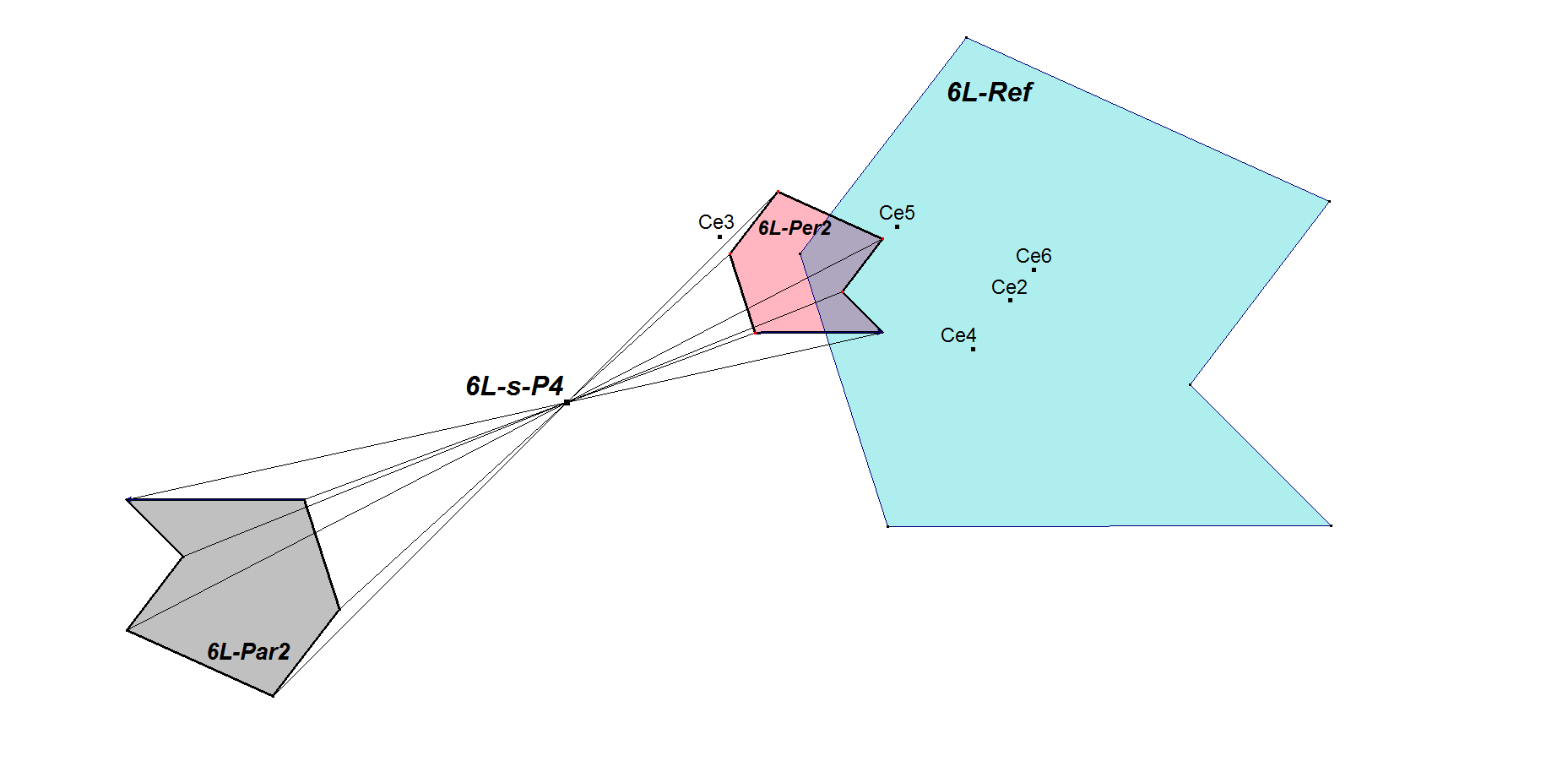
6L-s-P4: 6L-Conical Par2-Per2 Homothetic Center
In a 6-Line we have 6 Component 5-Lines.
When constructing 6 times the Inscribed Conic Centers (5L-s-P1) of the Component 5-Lines we get Ce1, … , Ce6.
By drawing lines through Ce1, … , Ce6 parallel to the omitted line (not used line of the 5-Line in the 6-Line) we get a 6-Line called 6L-Par1. Doing the same procedure for 6L-Par1 instead of the reference 6-Line 6L-Ref we get a 2nd generation 6-Line 6L-Par2.
By drawing lines through Ce1, … , Ce6 perpendicular to the omitted line (not used line of the 5-Line in the 6-Line) we get a 6-Line called 6L-Per1. Doing the same procedure for 6L-Per1 instead of the reference 6-Line we get a 2nd generation 6-Line 6L-Per2.
6L-Par2 is homothetic with 6L-Per2, giving rise to a Homothetic Center 6L-s-P4.
Properties
- The points
Estimated human page views: 289
