CO-Tf3 Scimemi Transformation
The Scimemi-transformation CO-Tf3 is a point-to-point mapping defined by a conic CO.This transformation and its action on pentagons was presented by Benedetto Scimemi at Feb. 2005 in Bloomington as a homage to Douglas Hofstadter for his 60th birthday.
This page has been written with the contribution of Benedetto Scimemi.
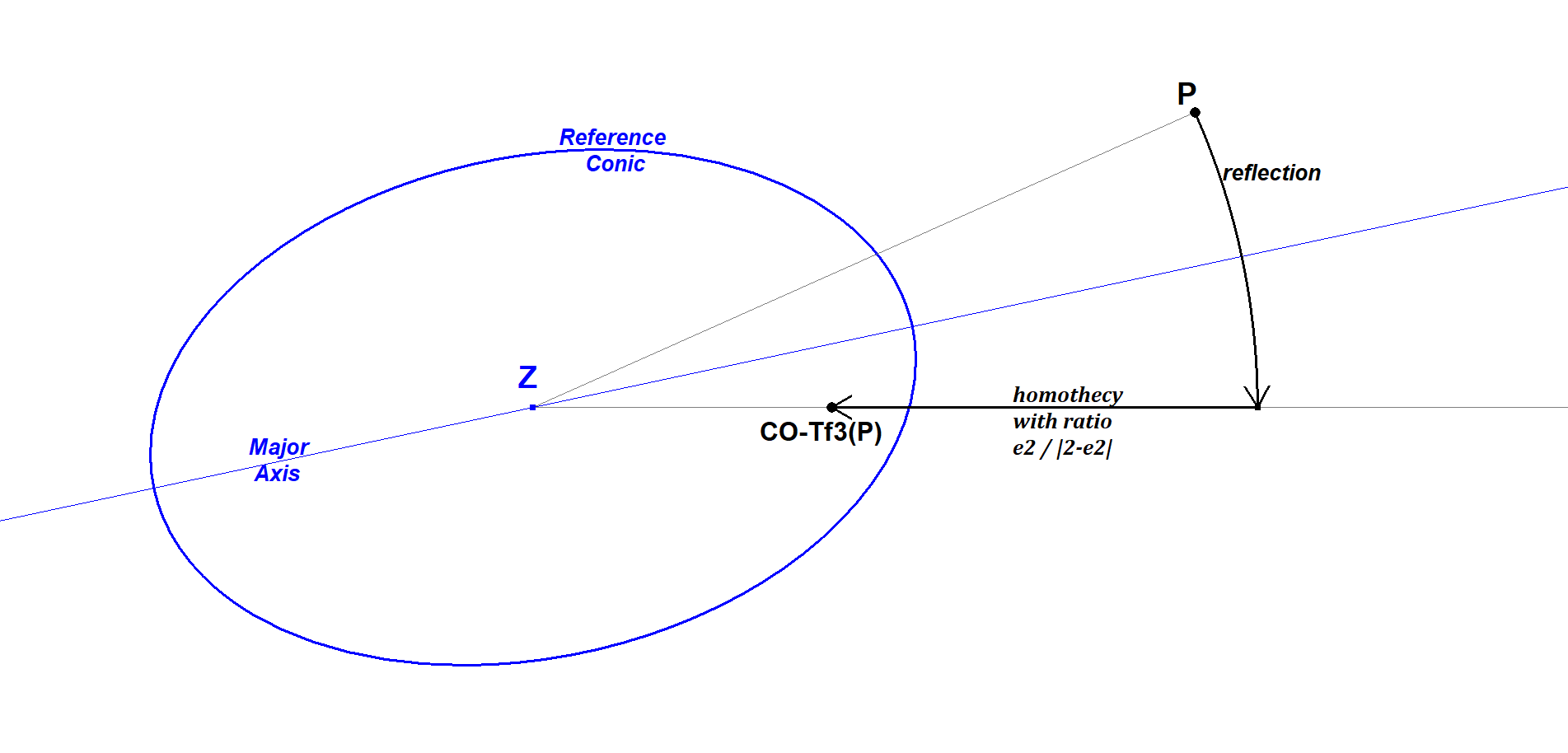
CO-Tf3 is defined wrt any conic CO, except circles and rectangular hyperbolas. Extensions to these cases, as limits, will be discussed below.For a central conic CO, the mapping P CO-Tf3(P) can be described as:
- a reflection of P about an axis of the conic, followed (or preceded) by
- a homothety with fixed point in the conic center Z and scale factor r > 0. The choice of the reflection axis and the value r only depend on the shape of the conic (i.e. they are the same for similar conics; see below).
When CO is a parabola the homothety is replaced by a translation.The mapping CO-Tf3-1 , the inverse CO-Tf3, has the same definition, provided the factor r is replaced by its inverse r-1.
It appears from the definition that
CO-Tf3 and CO-Tf3-1 are negative (odd) similarities.
Their fixed point is Z, their fixed lines are the CO-axes.
Notice that one gets the same mappings for Z-homothetic conics CO.
Definition
See [34], B. Scimemi, QFG#935 and #1252).
When CO is an Ellipse:
then CO-Tf3 is the product of the reflection in the major axis and the homothety, centered in Z, with scale factor (a2 – b2 )/ (a2 + b2). Here a > b are the axes lengths. Equivalently r = cos[α], where α is the angle under which a vertex views the minor axis.
When CO is a (non-orthogonal) Hyperbola:
call “principal” the axis which lies inside the smaller angle α formed by the asymptotes (N.B. not always the principal axis is the focal axis),
then CO-Tf3 is the product of the reflection in the principal axis and
the homothety, centered in Z, with scale factor r = (a2 + b2) / (a2 – b2 ), where a > bare the axes lengths. In this case r = cos-1 [α].
When CO is a Parabola:
then CO-Tf3 will be an isometry, the product of the reflection in the parabola axis and a parallel translation which amounts to twice the (oriented) distance directrix -> focus.
When CO is degenerated into two (non-orthogonal) lines crossing in Z:
then CO-Tf3 is the product of the reflection in the angle bisector of the smaller angle α formed by the lines; and the homothety, centered in Z, with scale factor cos [α].
When CO is degenerated into two parallel lines:
then CO-Tf3 is the reflection in the mid-line (parallel, equidistant).
Limit-cases
One can extend CO-Tf3 and by CO-Tf3-1, as limits, to orthogonal hyperbola and circles, but the resulting mappings are not invertible.
For an orthogonal hyperbola, CO-Tf3(P) tends the infinity point of the line Z.P, reflected in the principal axis; CO-Tf3-1(P) tends to the conic center for all P.
As for circles, CO-Tf3 maps each point P into the circle center; CO-Tf3-1 can’t be constructed.
Eccentricity
By introducing the eccentricity e, the homothety factor ((a2 −b2)/(a2 + b2))±1 can be unified into the single formula r = e2/|2−e2| holding for all types of conics.
See Ref-34, QFG#935 and #1252.
CO-Tf3 Chord Lemma
- This Chord Lemma is a basic property of Co-Tf3 (Benedetto Scimemi, 2018, February 8, personal mail).
- For any chord P1P2 of any conic CO, let M be its midpoint. Then then CO-Tf3(M) lies on the perpendicular bisector of P1P2 .
In particular, for any point P of CO, the normal to CO in P is the line P. CO-Tf3(P).
Conversely: For any point X, if the line through X normal to X.CO-Tf3(X) cuts CO in two (real) points P1, P2, then X is the midpoint of P1.P2.
Here are some consequences:
- Let Tr be any CO-inscribed triangle , O its circumcenter, N its ninepoint circle. Then O lies on the circle CO-Tf3(N).
- Let Tr be any triangle, O its circumcenter. For any conic CO circumscribed to Tr, the point CO-Tf3-1(O) lies on the nine-point circle of Tr.
- Let CO be a parabola, X1, X2 any points, Mi the midpoint of Xi . CO-Tf3(Xi). Then the line M1M2 is the axis of the parabola.
- For any quadrangle Q inscribed in any conic CO, the CO-Tf3 image of QA-P2 is QA-P4.
- For any pentangle PA = P1P2P3P4P5 let QAi the Component Quadrangle, obtained by ignoring the point Pi. Let Hi = QAi-P2, Oi = QAi-P4. Then the pentangles H1H2H3H4H5, O1O2O3O4O5 are negatively similar, the similarity being CO-Tf3 : Hi -> Oi, where CO is the conic circumscribing PA.
It was the proof of the last statement which gave origin to the whole subject of CO-Tf3.
Proofs of the above properties can be derived by synthetic arguments from the Chord Lemma. A proof of the Lemma itself is very easy if one represents CO by P = [a cos ∂, b sin ∂] or similar (see below, in the Section Coordinates).
Constructions
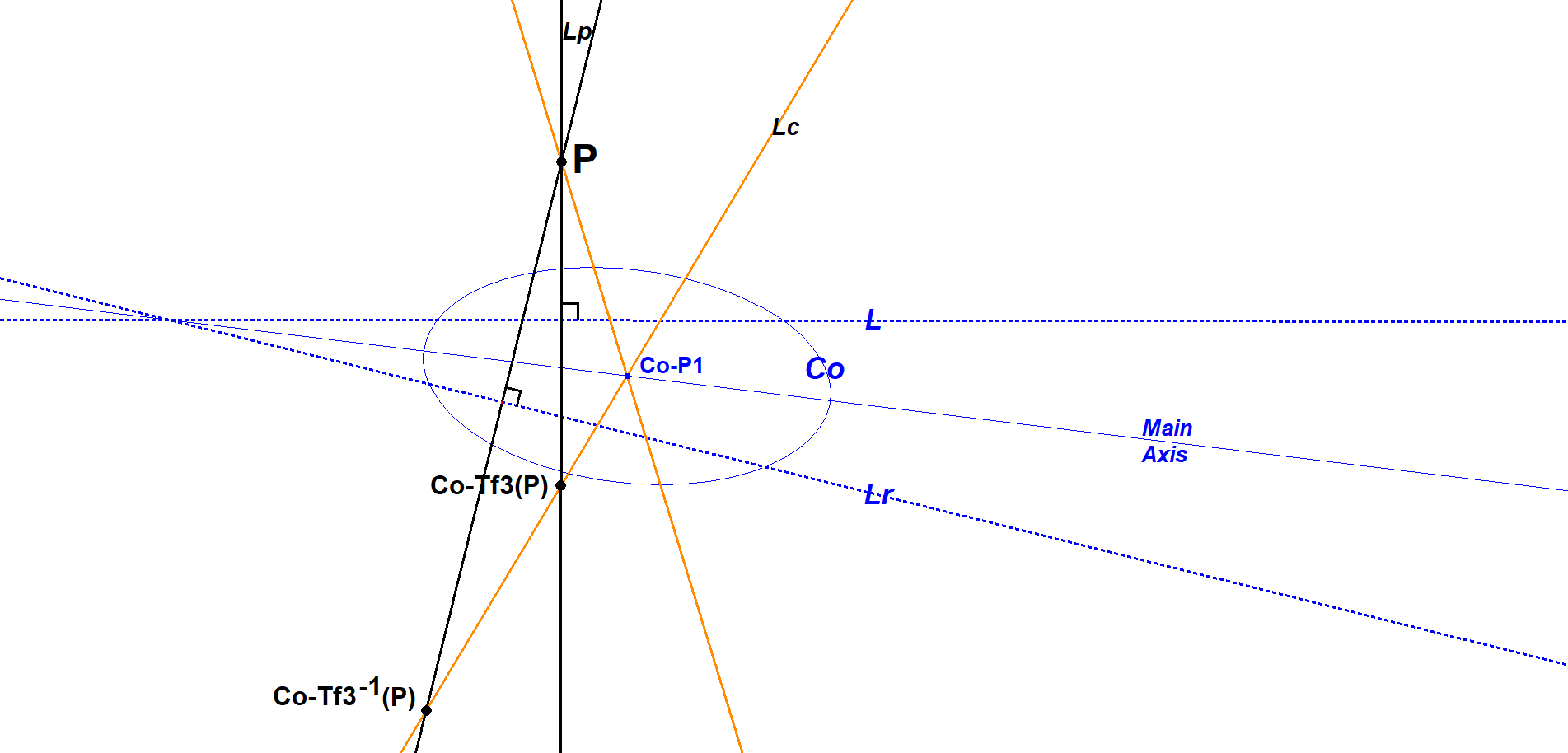
Schmidt-Construction for CO-Tf3(P)
This construction is based upon Eckart Schmidt’s construction at Ref-34, QFG#2811.
- Let L be the polar CO-Tf1 of P.
- Let Lp be the line through P perpendicular to L.
- Let Lc be the reflection of P.CO-P1 in the principal axis of CO.
- Finally CO-Tf3(P) = the intersection point of Lp and Lc.
Schmidt-Construction for CO-Tf3-1(P)
This construction was found by Eckart Schmidt. See Ref-34, QFG#2811.
- Let L be the polar CO-Tf1 of P.
- Let Lr be the reflection of L in the main axis of CO.
- Let Lp be the line through P perpendicular to Lr.
- Let Lc be the reflection of P.CO-P1 in the principal axis of CO.
- Finally CO-Tf3-1(P) = the intersection point of Lp and Lc.
Keizer-Construction for CO-Tf3(P)
This construction is based upon Bernard Keizer’s construction at Ref-34, QFG#2826.
- Let P1 be the inverse of P in the Orthoptic Circle CO-Ci2
- Let P2 be the inverse of P1 in the Circle CO-Ci1 with the foci as diameter
- CO-Tf3(P) = the reflection of P2 in the principal axis of CO.
Note: When the principal axis does not connect the foci, the orthoptic circle is not real. Replace it by the circle with radius (a2 – b2)1/2.
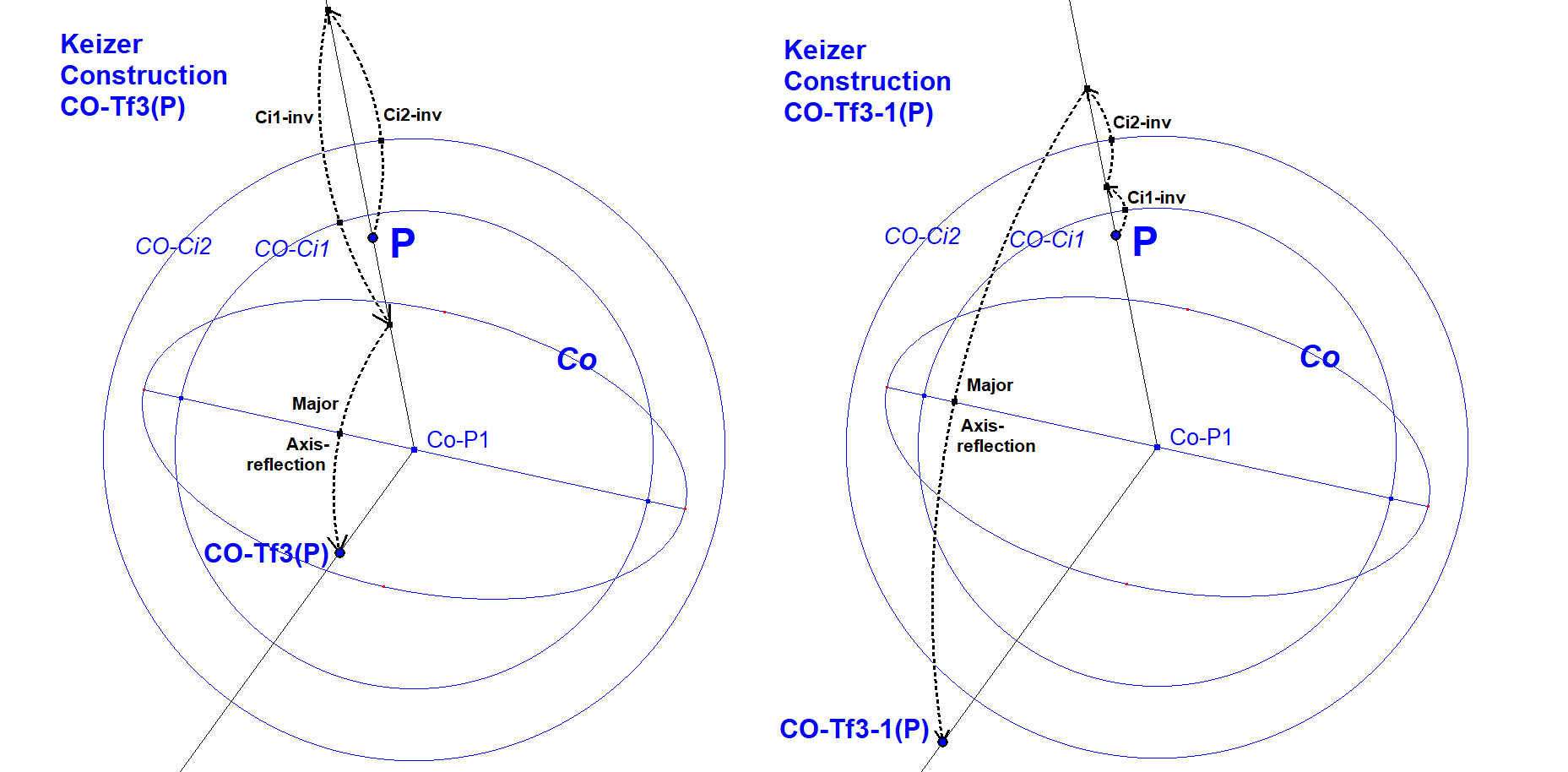
Keizer-Construction for CO-Tf3-1(P)
This construction is based upon Bernard Keizer’s construction at Ref-34, QFG#2826.
- Let P1 be the inverse of P in the Circle CO-Ci1 with the foci as diameter
- Let P2 be the inverse of P1 in the Orthoptic Circle CO-Ci2
- CO-Tf3-1(P) = the reflection of P2 in the principal axis of CO.
Note: When the principal axis does not connect the foci, the orthoptic circle is not real. Replace it by the circle with radius (a2 – b2)1/2.
Another Construction for CO-Tf3-1(P)
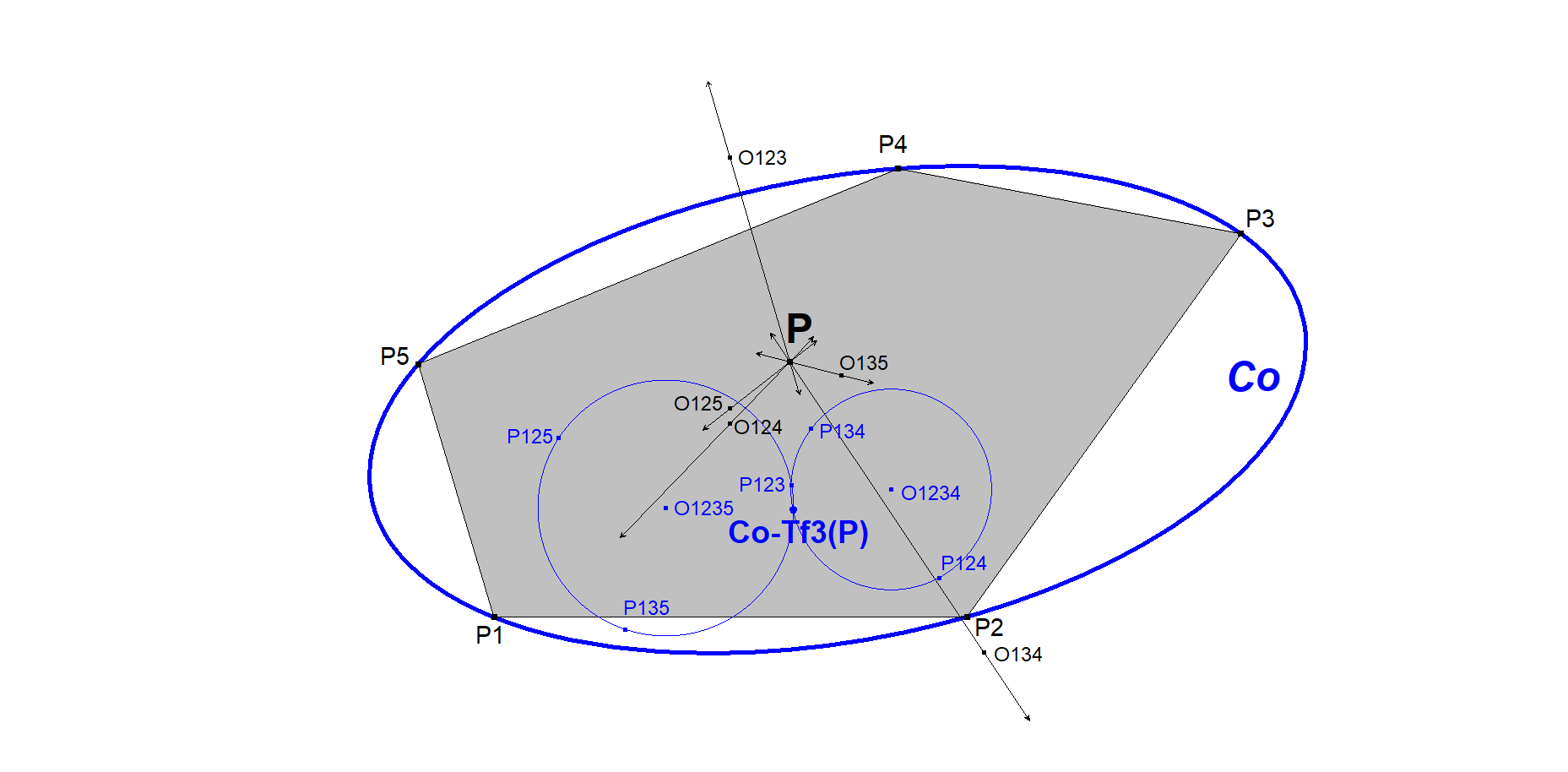
Next construction for CO-Tf3-1(P) is based upon the construction of 5P-s-Tf3, which is a construction of Telv Cohl. See [33], Anopolis #1986.
- Let P be the point to be transformed wrt some reference conic CO.
- Span some Pentangle P1.P2.P3.P4.P5 into Conic CO.
- Let Pijk be the Orthopole of line P.Oijk wrt triangle Pi.Pj.Pk (Oijk = center circumcircle Pi.Pj.Pk), where (i,j,k) are different numbers from (1,2,3,4,5).
- Let Ci1234 be the circle through P123, P124, P134, having center O1234.
- Let Ci1235 be the circle through P123, P125, P135, having center O1235.
- These circles have point P123 in common.
- CO-Tf3-1(P) will be the 2nd intersection point of Ci1234 and Ci1235.
Construction for CO-Tf3-1 from Benedetto Scimemi
(a quick recipe for CABRI and Geogebra users)
- Choose a circle Ci centered in P, such that CO and Ci have 4 intersections A1, A2, A3, A4. This is always possible when CO is a hyperbola; in other cases, it may be necessary to replace CO by a (larger or smaller) conic CO* obtained from CO by a convenient Z-homothety.
- Construct the centroid QA-P1 of the quadrangle QA = A1A2A3A4.
- Then P ~ QA-P4 and CO-Tf3-1(P) ~ QA-P2 will be the reflection of P on QA-P1 (QA-Centroid).
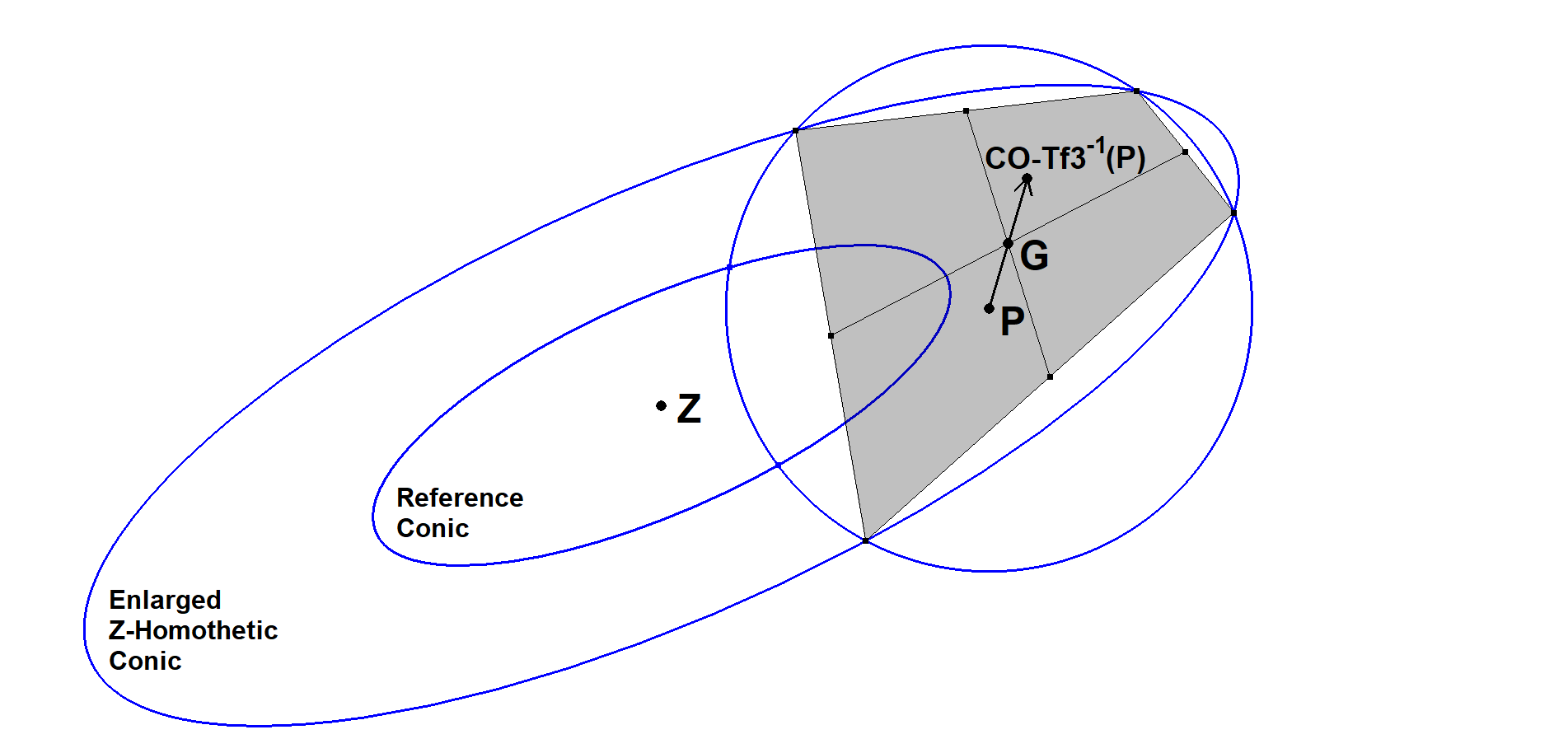
This construction is based on what can be considered the main property of CO-Tf3 / CO-Tf3-1:
they swap QA-P2 and QA-P4 for all quadrangles QA inscribed in CO (see the final Table).
Construction, when knowing CO-Tf3(P) or CO-Tf3-1(P), of their inverse
The construction of CO-Tf3-1(P) is, knowing the construction of CO-Tf3(P), very simple.
- Let Cix be the circle through P with center CO-P1.
- CO-Tf3R-1 (P) is the inverse of CO-Tf3(P) wrt Cix.
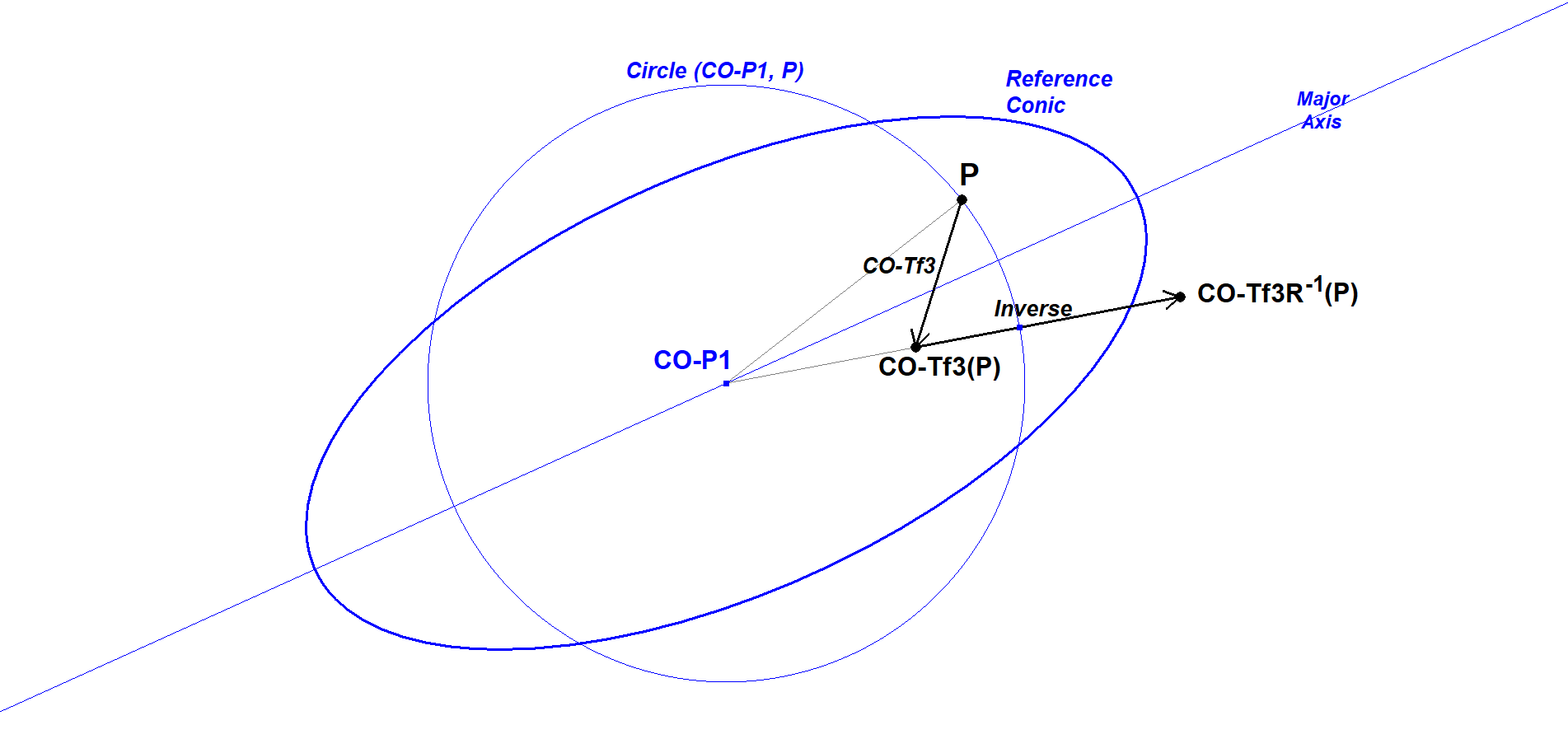
The construction of CO-Tf3(P), when knowing CO-Tf3-1(P), is identical.
Relationship with Frégier’s Point
For each point P on any Conic CO-Tf3(P) coincides with Frégier’s Point.
Frégier was a French mathematician who published several articles in the “Annales de Gergonne” around 1810. He discovered a remarkable point transformation with respect to a conic.
Let P be some point on conic CO. Draw a number of right angles having this point as their vertices. Then the intersected chords have in common a point, being called Frégier’s Point. See Ref-13, keyword “Frégier’s Theorem”.
Frégier’s Point is only defined for points on a conic. CO-Tf3 is defined for all points in the plane.
This makes CO-Tf3 a generalization of Frégier’s Point.
Relationship with Orthotransversal Line and Pedal Circle wrt a CO-inscribed Triangle
For any CO-inscribed triangle Tr and any P on CO:
- CO-Tf3(P) lies on the orthotransversal line of P w.r.t. Tr
- CO-Tf3-1(P) lies on the pedal circle of P w.r.t. Tr.
Therefore, given any two triangles inscribed in the same conic CO, the two orthotransversal lines of P meet in CO-Tf3(P), the two pedal circles of P meet in CO-Tf3-1(P). In particular, this holds when we deal with Component Triangles of a Quadrangle and it proves (by choosing CO circumscribed to the Quadrangle and passing through P) that
(1) the 4 orthotransversal lines have a common point. See Ref-59, AoPS, VU Thanh Tung, 2015, June 26 and Ref-34, QFG#1233).
(2) the 4 pedal circles have a common point. See Ref-59, AoPS, Luis Gonzales, 2011, August 7 and Ref-34, QFG#1218).
For a description of the connection of both properties see Ref-34, QFG#1252, Benedetto Scimemi, August 2015).
Barycentric Coordinates
Let Reference Conic CO be defined by 5 points (1:0:0), (0:1:0), (0:0:1), (p:q:r), (u:v:w),
then CO has equation X y z + Y z x + Z x y,
where X = p u (q w – r v), Y = q v (r u – p w), Z = r w (p v – q u).
and CO-Tf3[(x:y:z)] will have these barycentric coordinates:
( X (+a2 (x + y + z) – b2 (x + y – z) – c2 (x – y + z)) – 2 a2 (Y z + y Z) :
Y ( -a2 (x + y – z) + b2 (x + y + z) + c2 (x – y – z)) – 2 b2 (X z + x Z) :
Z ( -a2 (x – y + z) + b2 (x – y – z) + c2 (x + y + z)) – 2 c2 (X y + x Y) )
The barycentric coordinates of CO-Tf3-1[(x:y:z)] are much longer.
Cartesian Coordinates
Cartesian Coordinates for both of CO-Tf3 and CO-Tf3-1 are very easily written if one represents CO by P = [a cos δ, b sin δ] for ellipses or [a / cos δ, b tan δ] for hyperbolas.
Then CO-Tf3([x,y]) = [x, – y]((a2 -b2)/(a2 + b2 ))±1.
If CO is the parabola y = x2 then CO-Tf3( [x,y] ) = [-x, y+1].
Examples of CO-Tf3 and CO-Tf3-1 Transformations
The action of CO-Tf3 can be read from left to right.
The action of CO-Tf3-1 can be read from right to left.
| Ref.system | Reference Conic | point-1 | point-2 | point-3 |
|---|---|---|---|---|
| Triangle | Steiner Inellipse / Circumellipse | X(5988) | X(1) | |
| X(2) | X(2) | X(2) | ||
| X(114) | X(3) | X(1352) | ||
| X(98) | X(4) | X(6776) | ||
| X(6036) | X(5) | X(182) | ||
| X(115) | X(6) | X(2549) | ||
| X(1281) | X(8) | |||
| X(10) | X(3923) | |||
| X(11) | X(5091) | |||
| X(6109) | X(13) | X(10654) | ||
| X(6108) | X(14) | X(10653) | ||
| X(6115) | X(15) | |||
| X(6114) | X(16) | |||
| X(1513) | X(98) | |||
| X(230) | X(115) | |||
| Quadrangle | Any Conic circumscribing Reference Quadrangle | QA-P2 | QA-P4 | |
| QA-Co1 | QA-P6 | QA-P2 | ||
| QA-P23 | QA-P36 | QA-P11 | ||
| QA-L1 | QA-L4 | QA-L1 | ||
| QA-Lx *) | QA-L2 | |||
| QA-Co3 | QA-P23 | QA-P6 | ||
| QA-P30 | QA-P12 | |||
| QA-P3.QA-P4 | QA-L1 | |||
| QA-P2.QA-P23 | QA-L2 | |||
| QA-Ly *) | QA-L4 | |||
| QA-L8 | QA-L8 | |||
| Pentangle | Circumscribed Conic of Pentangle | 5P-s-P1 | 5P-s-P1 | |
| 5P-s-Px **) | 5P-s-Py **) |
*)QA-Lx = line through QA-P6 parallel to QA-P2.QA-P23
QA-Ly = line through QA-P23 parallel to QA-L1
**)5P-s-Px = Conic Center of the five 5P-versions of QA-P2
5P-s-Py = Conic Center of the five 5P-versions of QA-P4
Warning: In a Pentangle the Scimemi Transformation CO-Tf3 wrt the circumscribed conic is identical to the inverse of the 5P-s-Tf3 Transformation.
These results were found by Eckart Schmidt, Benedetto Scimemi and the author of EPG.
There will be probably many more appealing examples.
Estimated human page views: 349
